Dr. Stephen F. Sontum
Thesis
Advisor
Submitted in partial fulfillment of the requirements
for
Honors
in
Chemistry and Biochemistry
Middlebury
College
Approved:
&nbp;
Committee
in Charge
Table of contents in HTML format
Abstract
The Spiro and Kitagawa groups have made two different sets of frequency assignments for the bending frequency of carbon monoxide in carboxymyoglobin. A computational resolution to this controversy has been attempted in this thesis by developing a force field for the heme porphyrin (protoporphyrin IX). Our analyses support the Spiro group's assignment of 574 cm-1 to this bending frequency. The successful development of the heme force field was done by transferring over force fields developed for smaller molecules like nickel octaethyl porphyrin (NiOEP), ethylbenzene and benzene.Trends observed in such analysis recommend the use of specific dihedral terms for modeling out of plane motions, and expansion of the dihedral set to model ethyl groups attached to aromatic systems Furthermore, exclusion of improper torsion terms in the potential equation is suggested unless hyperconjugation effects need to be simulated. Finally, an alternative approach to modeling strained systems is developed, in which unstrained values for structural parameters are used.
Nur die Fülle führt die Klarheit,
Denn im Abgrund wohnt die Wahrheit!
(Frederich Schiller)
Literally translated, this famous saying of Schiller's would mean, "only completeness leads to clarity because the truth lies in an abyss". According to Schiller in order to determine the truth the entire picture is needed. Only with such a 'completed' picture is it possible to discard plausible explanations in favor of the correct explanation, and be certain that the truth, wherever it may be, has been discovered.
This saying is particularly appropriate in molecular spectroscopy, where spectra provide insights into real molecules, and one needs to see the 'entire' picture to be confident of one's interpretations of a spectrum. There are often a variety of possible explanations, and hence disputes persist regarding the interpretation of such spectral data. This thesis is an attempt towards resolving one such dispute.
The focus of this thesis is to computationally probe the vibrations of carboxyheme in the hope of identifying the bending frequency of the carboxyheme linkage. A computational approach will be taken, so that an alternate method is available to reproduce experimental results. Successful assignment of this bending band, in turn, will allow an estimation of the energy required to bend the iron-carbon linkage, and resolve a controversy surrounding the interpretations of carboxymyoglobin spectra.
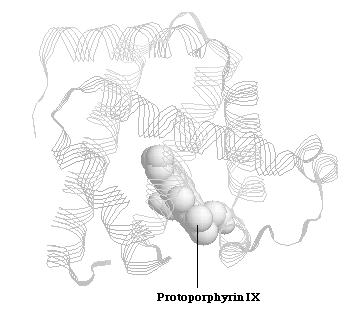
Myglobin is a relatively small sized protein, which has a single polypeptide chain containing 153 amino-acid residues.Myoglobin's primary function is oxygen storage, and it is particularly abundant in diving mammals such as whales and seals. X-ray crystal structures reveal that the backbone of the myoglobin molecule consists of eight relatively straight structure segments set off by bends (Figure 1.1). 1 This structure is similar to subunits of another protein, hemoglobin. The same heme group (Protoporphyrin IX), from which both proteins derive their oxygen transporting and storing properties, is noncovalently bound to the interior of myoglobin and hemoglobin. 1

Figure 1.1 Spermwhale Myoglobin and Protoporphyrin IX Core
The heme group belongs to the most abundant class of porphyrin derivatives known as protoporphyrins. Protoporphyrins consist of four pyrrole rings bound to a central metal atom, four methyl groups, two vinyl groups and two propionic acid groups. In protoporphyrin IX, the four pyrrole groups bind to iron metal center to form a square planar complex. Two more ligands can attach at the axial positions, one of which, in myoglobin, is nitrogen from a proximal-side histadine (His 64) residue (Figure 1.2). 1 The final, axial ligand varies, and determines the function of heme. In myoglobin, this sixth ligand is dioxygen allowing this protein to store oxygen.
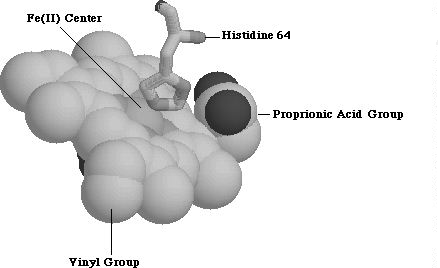
Figure 1.2 Protoporphyrin IX along with Histidine 64 Residue
Apart from the dioxygen ligand, the iron metal center of the heme porphyrin can bind to other gaseous ligands, of which carbon monoxide is a particularly important example. Carbon monoxide is often used as a substitute for the dioxygen ligand in spectroscopic studies of heme, since both these gases bind to heme forming low-spin complexes, which induce similar changes in the protein structure. 2 However, carbon monoxide has the advantage of possessing a permanent dipole, which allows the ligand to be followed through resonance Raman and infrared spectroscopy. Therefore, the carbon monoxide ligand is used to probe "structure-function" relationships between oxygen and heme. 3
Despite these aforementioned similarities, it is also known that these two ligands differ in their electronic structure and modes of binding. The binding affinity of carbon monoxide to heme is extremely environment sensitive, as the residues surrounding heme control the porphyrin's binding affinity to carbon monoxide. While CO binds 103 ~ 104 times more strongly than oxygen to free heme porphyrins, 4 within the myoglobin protein environment carbon monoxide binds only 30 times stronger that the dioxygen ligand.
The cause of this environment controlled difference in binding affinities of CO has been the object of much debate. 5 The original X-ray structures of a sperm-whale myoglobin bound to CO ligand was interpreted to indicate that the Fe-C-O angle of binding was not linear, as in the free heme porphyrin, 6 but rather bent. 7 The argument, therefore, was that the protein imposed steric hindrances on the binding of CO ligand, forcing it to bind in a bent fashion. As a bent binding structure is not favorable for backbonding between the Fe dxy and CO [[pi]]* orbitals (Figure 1.3), the binding affinity is reduced. In the case of the oxygen binding, the angle of binding of the ligand to the heme porphyrin is bent, irrespective of whether the porphyrin was within the protein environment or not. 5 Therefore, its binding affinity is not affected by the protein environment.
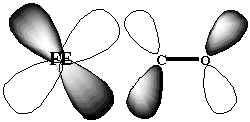
Figure 1.3 Backbonding possible between dxy and [[pi]]* orbitals.
While this explanation seems plausible at first glance, some deficiencies of this model have been pointed out. Anfinrud and coworkers concluded, using the technique of photo-selection spectroscopy, that the Fe-C-O geometry is nearly linear under physiologically relevant conditions. 8 Spiro and coworkers point to the prohibitive cost of distorting the Fe-C-O angle away from linear. Reduction of binding overlap resulting from bending the Fe-C-O linkage would increase the energy of the Fe-C-O linkage. This energy could not possibly be supplied by the protein matrix, which would more likely adopt a different conformer. 5 Finally, recent X-ray structure determinations of other forms of myoglobin indicate that the angle of CO ligand binding to the Fe (II) center is around 169[[ring]], 9 and not between 120-140[[ring]] as in the sperm whale myoglobin. 7 As yet the actual cause of this differential binding is not fully known. Other factors proposed include the displacement of the iron atom from the heme plane, electrostatic interactions between the ligand and its surroundings in the heme pocket, the solvent content, and the polarity of the distal pocket. 9
An important argument against the bent FeCO model involves the energy required to bend the FeCO linkage. Spiro and coworkers indicate that this energy is too large to allow the sterically hindered model. A rough measure of this energy could be obtained from the FeCO bending frequency. This mode of vibration corresponds to the energy required to bend the FeCO linkage and reflects the amount of destabilization caused by moving away from the linear FeCO model (Figure 1.4a). However, there exists a disagreement over the assignment of the vibrational frequency caused by this bending motion. The Spiro and Kitagawa groups make particularly compelling cases for different assignments of this frequency. Since resolution of this controversy will be the focus of this study, it is necessary to explain the rationale behind their different assignments.
Spiro's group 2 analyzed resonance infrared spectral data obtained from model metalloporphyrin-carbon monoxide systems. They assigned a band at 574 cm-1 to the bending motion of the Fe-C-O, and another band at 494 cm-1 to the stretching motion of Fe-C. Their reasoning is that the band at 574 cm-1 displays a "zig-zag" decrease in frequency when different, isotopically substituted carbon monoxide ligands are used. 10 Specifically, while this band is very sensitive to changes in the weight of the carbon atom in the carbon monoxide ligand, it is less sensitive to changes in the mass of the oxygen atom. As Figure 1.4 shows, in the bending mode of the FeCO linkage, the carbon atom experiences the maximum displacement, while the oxygen atom remains relatively stationary. Therefore, the 574 cm-1 band was assigned to the bending of the carbon monoxide ligand. The band at 494 cm-1 displays a monotonous decrease in frequency; decreasing as the weight of the carbon monoxide increases. Furthermore, the shift in this bands frequency is not as sensitive as the 574 cm-1 band to changes in the mass of the carbon atom. This frequency shifting pattern is expected for the stretching motion of Fe-CO bond, in which the entire CO unit undergoes displacement. The 494 cm-1 band was assigned to the stretching motion of the Fe-CO linkage.

Figure 1.4 Motion of CO in Bending and Stretching Modes
a. Only Carbon atom moves in d(FeCO) bending motion.
b. The entire CO unit moves in [[upsilon]](FeCO) stretching motion.
The reasoning behind this unusually high assignment (574 cm-1) for a bending frequency (even higher than the corresponding stretching frequency mode at 494 cm-1) involves a strong back-bonding argument. Spiro used this argument to disprove the idea of having a sterically bent Fe-C-O set up within the myoglobin protein environment (Figure 1.3). 5 This resistance is reflected in the high bending constants, which would follow from a high 574 cm-1 frequency assignment to the bending frequency. On the other hand, the stretching of the Fe-C linkage does not destroy the backbonding overlap. As it is energetically less demanding than the bending motion of the ligand bound to the porphyrin, the stretching frequency itself is below that of the bending motion.
The primary focus of the Kitagawa group 11,12 is the analysis of the heme porphyrin in its bound state to the CO ligand within its protein environment. They contend that the assignment of the 574 cm-1 band is better explained as a combination band of the Fe-C-O bending mode (360 cm-1), and an internal porphyrin skeletal mode (200 cm-1). 13 The fundamental band at 360 cm-1 is very weak in intensity and is submerged within other, much stronger bands seen in that region. This group also uses isotopic shift data to identify this bending motion. The characteristic "zig-zag" pattern that Spiro's group used to justify their assignment of the band at 574 cm-1 as a bending mode, is also observed for this 360 cm-1 band. However, the shift in frequency seen is much smaller for the 360 cm-1 band than that seen for the 574 cm-1 band. Selection rule arguments, which forbid the FeCO fundamental bending mode from being resonance Raman active, are used to rule out the Spiro group assignment of the 574 cm-1 band as being a fundamental bending mode. Any combination band or overtone of a fundamental, however, can be RR active. As the Kitagawa group observed the 574 cm-1 band using resonance Raman spectroscopy, this frequency was assigned as a combination mode. Having assigned the 574 cm-1 band as an overtone, the Kitagawa group then assigns a band at 360 cm-1 to be the fundamental bending motion of the Fe-C-O linkage. This assignment allows the bending frequency to be lower than the corresponding stretching frequency.
Ab initio calculations done by Kitagawa's group on a simplified 2 amidinato ligand system, 14 indicate that the energy required to bend the Fe-C-O bond is not so large that it could not be bent by steric interactions. Consequently, it was possible to assign a lower frequency (360 cm-1) frequency to this bending interaction.
As a another twist to this controversy, the 360 cm-1 band identified as the bending fundamental by Kitagawa finds a different assignment in Spiro's work. This band is assigned by Spiro et al. to an internal porphyrin motion coupled to the the CO ligand's motions.
One of the key differences between the arguments provided by Kitagawa's and Spiro's groups is that Spiro's observations were drawn from model compounds outside the myoglobin environment, while Kitagawa's conclusions were drawn from spectroscopic data obtained of heme complexes within the protein environment. As such it is impossible to determine the validity of either one of their assignments on the merits of their arguments alone. Each of their respective conclusions are consistent with the spectroscopic evidence they provide. In addition, as the actual spectroscopic conditions themselves are different, it is not possible to reconcile their difference in the conclusions from experimental data alone.
In such cases a molecular model, which accurately simulated the vibrational and structural characteristics of the carboxyheme porphyrin would clearly be useful. The Spiro/ Kitagawa controversy regarding FeCO bending frequency, could be resolved by computationally recreating the isotopic-shift experiments done by both the Spiro and Kitagawa groups. Not only could the carbon-isotope sensitive bands be determined, but also the types of motions causing these bands be identified. Thus the correct FeCO bending frequency could be identified, and the effects of the protein environment on this band can be evaluated.
For spectroscopic purposes two particular types of modeling systems, vibrational and molecular mechanic force fields, have become predominant among biochemical and organic chemists. 15 These modeling systems are referred to as force fields because they use analytical potential energy functions, within the framework of classical mechanics, to predict restoring forces and the vibrational frequencies of the modeled molecules. Of these two methods the method of molecular dynamics has been adopted in this thesis, as it allows easier transfer of force fields between similar molecules. Therefore, a description of the molecular dynamics force-field is done with the understanding that there exists another modeling philosophy.
Most force fields 16 build of off the assumption that the molecule is at its minimum energy, and that it is only slightly perturbed from this minimum energy configuration. The resulting potential function can be described by a harmonic function (linear dependence on a square term) between the perturbation and the corresponding restoring force. Use of Newton's equation of motion establishes secular equations between observed frequencies and these restoring force constants. Given a set of force constants, the vibrational frequencies can be calculated by solving for the eigenvalues corresponding to the matrix of these secular equations. 17 The force constants are then varied until the calculated frequencies correspond to the experimentally observed ones. At the end of such force-constant optimization, a consistent force field is said to have been obtained, as this force field is consistent with experimentally observed data.
The actual molecular mechanics program used in this thesis is called AMBER (Assisted Molecular Building with Energy Refinement). Peter Kollman, in creating the AMBER model for generating molecular mechanics force fields, placed an emphasis on more "explicitly stated algorithms". 18 Parameters developed using this program, therefore, are done so with explicit information regarding their transferability. As this thesis aims to develop a force field for protoporphyrin IX using data obtained from other, simpler molecules, the AMBER molecular mechanics package was chosen. Futhermore, this package allows analysis of the internal coordinates or parameters responsible for each of the frequency. This added information will help in identifying the frequency of the FeCO bending motion.
Li and Marques 19-22 used different force fields to model the heme porphyrin. Marques parametrized iron porphyrins using molecular dynamic force fields, but concentrated on representing the actual shapes of various heme porphyrin as given by their crystal structures. Thus Marques' emphasis allowed him to calculate and accurately predict the geometry of various heme complexes depending on the stress placed on them.
Li on the other hand, chose to concentrate on modeling vibrational features of nickel octaethyl porphyrin (NiOEP) (Figure 1.6 ). He used a vibrational force to classify the vibrations according to their normal modes. He modeled the NiOEP molecule because it is structurally similar to the heme porphyrin. Although NiOEP has a different metal center, it has the same porphyrin core as protoporphyrin IX. The advantage of using NiOEP, however, is that it is easier to obtain pure and isolated from the myoglobin protein. Li succeeded in breaking the various motions into in-plane and out-of-plane motions. He concluded that such a model could then be used to model the interactions of the heme itself. At 360 cm-1 he observed an out-of-plane (OOP) frequency which he assigned to the a doming motion of the porphyrin (Figure 1.7). He suggested that this frequency could be important in the dynamics of the protein-ligand interactions, as this OOP mode could couple with motions of the ligands.
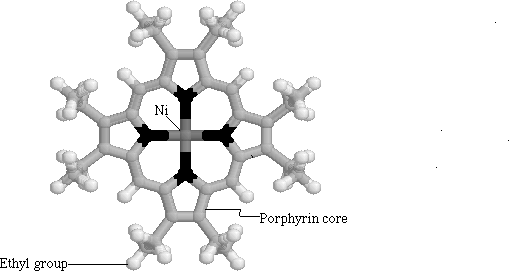 Figure
1.6 Nickel Octaethyl Porphyrin
Figure
1.6 Nickel Octaethyl Porphyrin

Figure 1.7 Out of Plane Motion of NiOEP at 360 cm-1.
The general goal of this thesis project, that of developing of a model to describe the interactions of CO with the heme porphyrin, builds of off the studies done by Li and Marquis. The force field aimed for in this thesis should accurately represent both the actual geometry and the vibrational features of heme porphyrin.
Specifically, the force field developed by Maggie Zraly and Jason Dimmig will be optimized. 23,24 Jason Dimmig succeeded in optimizating of the in plane vibrations of the NiOEP against the vibrational data obtained by Li. The out-of-plane (OOP) modes however, are still left to be optimized. Optimization of parameters describing these modes of vibrations will be the immediate focus of this thesis. As a molecular dynamic force field is being used, the fully-optimized parameters for NiOEP should transfer over to Protoporphyrin IX. The transferability of these parameters will tested against the structural data of various other porphyrins. If these parameters are truly transferable, then they should reproduce the structural characteristics of these other porphyrin, in different environments. Thereafter these parameters will be transferred over to the heme porphyrin itself, and due allowances will be made for the structural differences between the protoporphyrin and NiOEP. Parametrizing the heme porphyrin with parameters from NiOEP should be relatively easy. Only the additional groups would have to parametrized; and even these parameters could be transferred from other smaller and simpler molecules.
From the force field thus obtained, the various frequencies of the porphyrin bound to the CO will be calculated. The Spiro/Kitagawa controversy will be addressed by computationally recreating the isotopic-shift experiments that both these groups have performed. The FeCO bend band will be identified within and outside of the myoglobin protein, and the effects of the protein environment will be examined. Such analysis will help complete the "picture" of the vibration spectrum of the heme porphyrin, and allow clearer understanding of the real molecule, whose vibrations are represented in the carboxyheme vibration spectrum.
The primary goal of this project, that of analyzing the normal modes of vibration of carboxymyoglobin, required the development of a force field, which accurately reproduced the vibrational and structural features of this porphyrin. The general philosophy of this project has been to develop consistent force fields for smaller molecules and transfer these force fields to larger molecules until it was possible to model protoporphyrin IX itself. It was hoped that this approach would allow testing of new modeling methods on smaller molecules, in which the smaller numbers of variables and vibrational frequencies make such testing tractable.
As transferability of parameters was critical to this project, a molecular mechanics package was chosen. Inherently, molecular mechanics packages allow easier transfer of force fields between molecules. Furthermore, a well-tested, modeling package was sought that used explicitly stated algorithms. Limitations of such a model would be known and unrealistic levels of accuracy would not be aspired for. Lastly, the mechanics package needed to be flexible enough, to allow transfer of molecules into a protein environment.
The AMBER 4.1 software, 25 developed by the research groups of Peter Kollman and David Case, satisfied the aforementioned requirements and was used to create the porphyrin force field. This software program was designed to perform molecular dynamics calculations on protein, and has programmed into it general force fields for proteins. Therefore, upon development of a consistent force-field for the carboxyheme porphyrin, it would be possible to transfer the porphyrin force field into the protein environment. Analysis of the Fe-CO bending motions (d(FeCO)) could then be performed outside and inside the myoglobin protein.
The version of AMBER, AMBER 4.1, used in this thesis is an updated version of the software used by Jason Dimmig to model nickel porphine (NiP). It retains all the features described by Jason Dimmig in his thesis. A short summary of these features will given here, as the details may be obtained elsewhere. 25
The AMBER 4.1 package consists of different modules, which allow users to input a molecule's structure and internal parameters, move the molecule to its lowest energy structure, and then calculate the normal modes associated with this equilibrated structure. The PREP, LINK, EDIT and PARM modules allow the user to build the molecule. The SANDER module minimizes the molecule to its equilibrium structure, and the NMODE and NMANAL modules compute and classify the normal mode frequencies (orbitals) associated with this structure.
In the PREP module the internal topology of a molecule is defined. Parameters used to describe this topology include bond distances, bond angles and proper torsion (dihedral) angles between adjacent atoms. Figure 2.1 show a part of the internal topology, which would be generated by the PREP module to describe the connectivity between six atoms. Improper torsion terms, which help maintain the planarity in a molecule, are usually defined between four non-consecutive atoms. As ambiguity exists regarding improper torsion parameters, these parameters need to be explicitly stated. Therefore, the desired improper terms are explicitly listed at the end of the PREP file. A separate PREP file is needed for each different residue in a molecule. As AMBER 4.1 has PREP files for standard amino-acid residues, new PREP files were only created for non-standard residues (like NiOEP and heme porphyrin). All the non-standard prep files used are listed in Appendix A.

Figure 2.1 Internal Topology defined by the PREP module.
Bond Stretch between atoms 1 & 2.
Angle Bending between atoms 1, 2, & 3.
Proper Dihedral torsion between atoms 6, 1, 2, & 4.
Improper Torsion (Explicitly defined) between atoms 5, 1, 6, & 2.
After the various PREP files were created, the LINK module was used to connect the individual residue PREP files. In the LINK input file, the residues are listed in the order that they need to be connected. A protein chain results from connecting standard residues. Non-standard residues like the heme porphyrin are also connected to proteins using the LINK module.
As the LINK module writes out the molecular topology only in terms of the molecules internal parameters, the EDIT module is required to fix the location of the atoms in Cartesian coordinate space. The EDIT module takes the output from the LINK module, and transforms the molecule's coordinates from internal to cartesian (x, y, and z) ones. Protein Database (PDB) files are usually used by the EDIT module as a reference, with which to place the atoms in Cartesian coordinate space. The PDB files for the heme porphyrin were extracted from PDB files of myoglobin. The porphyrin coordinates were rotated and translated so that the metal center was located at the origin. The porphyrin plane was oriented parallel to the xy plane, such that the z direction was perpendicular to the porphyrin plane. All PDB files used in this thesis have been listed in Appendix B.
Atoms in the EDIT input file are with those in the PDB file using unique atom labels specified in the PDB and PREP files, and then missing atoms are filled in. In defining the porphyrins, opposite pyrrole ring nitrogens were defined the same, while adjacent ones had different labels. Thus, two sets of atom labels were used for the pyrrole nitrogen atoms. Once the matching of atoms labels has been completed, a new PDB file is written out by the EDIT module. Finally, a topology file describing the connectivity of the residues is also created by the EDIT module.
The topology output from the EDIT module serves as an input to the PARM module. The PARM module assigns parameters to the various internal coordinates of the molecules determined by the previous modules. Values for these internal parameters are taken either from standard AMBER files or user-defined "frcmod" files. The output file (prmtop file) generated by the PARM module contains information on both the connectivity as well as the parameters describing the molecule's topology. This output is used by other AMBER modules. The sets of values for the internal parameters which is are used by the PARM module is the force field that one seeks to optimize for molecules. Values for parameters that were not optimized were taken from the standard AMBER force field. 18
Vibration frequency calculations require that a molecule be at its energetic minimum (equilibrium structure), in order for harmonic approximations to be valid. Therefore, before any vibration analysis could be done, the SANDER module was used to minimize the energy of the molecule. This module uses a first-derivative, conjugate-gradient algorithm to arrive at a minimum energy structure. The atoms defined by the PARM and EDIT modules are relaxed along a potential gradient, until an energetically minimized structure is reached. Minimization was stopped when the this gradient fell below 10-4 kcal Å-1. While this minimization technique is effective for proteins, it is not sensitive enough to reach a minimum structure for porphyrins and other smaller molecules modeled in this thesis. After minimizing with the SANDER module, a second-derivative, Newton-Raphson minimization technique was utilized to lock in onto the local minimum structures for these smaller molecules. The stopping criteria with this method could be more stringent than, and therefore, minimization was stopped when the potential gradient fell below 10-5 kcal Å-1. This combination of first and second derivative techniques was chosen, as a second-derivative technique is likely to diverge if the molecule is not near equilibrium 15.
After minimization, the NMODE was used to calculate the various normal modes of the molecule, and the NMANAL module was used to analyze these normal modes.
Molecular Mechanics Force Fields
The AMBER force field evolves out of the following potential energy function.
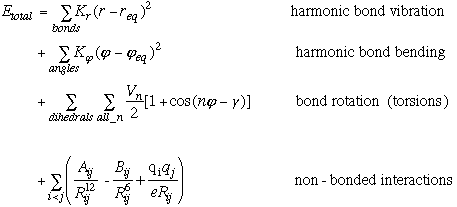
Equation 2.1 AMBER Potential Equation.
The first two terms represent the classical physics, harmonic approximation that is made in a molecular mechanics models. Perturbations away from equilibrium are resisted by a restoring force, which raises the potential energy of the molecule. This rise in potential energy depends both on the restoring force constant (Kr or K[[phi]]) as well as the square of the perturbation away from equilibrium. Therefore, the values of Kr and K[[phi]] are dependent on the choice of req and [[phi]]eq values. In this thesis, two modeling approaches were employed, each of which exploited the interdependance of force constants and equilibrium values in different ways.
Sundar/Sontum_old Modeling Method
In the first method, req and [[phi]]eq values were taken from X-ray crystal structures of the molecules. Therefore for NiOEP, crystal structure values used by Li et. al. were used. The force constants were then varied to obtain a good vibrational fit. Finally, the structural parameters were again varied till a good structural fit was also obtained. The emphasis of this method was to obtain vibrational fits by varying the force constants, while a geometric fit was obtained by mostly varying the equilibrium structural (req and [[phi]]eq) constants.
Sundar/Sontum_new Modeling Approach
The second approach was fundamentally different from the previous one, as force constants were also varied to get a good geometric fit. Instead of crystal structure values,.equilibrium bond distances (req and [[phi]]eq) were set to unstrained bond lengths, while equilibrium angles were set using hybridization arguments. Therefore, the Ni-N and Fe-N bond lengths were set to 1.86 Å and 1.93 Å respectively. 26,27 Other bond lengths within the porphyrin were set using bond order arguments and a linear scaling formula developed by Kollman et. al. 18 Using this formula the CC-CB, CC-N, CB-CB, CC-CD distances were set to 1.38, 1.38, 1.35, 1.44 Å respectively. All sp2 and sp3 hyridized-atom equilibrium angles were set to 120deg. and 109.5deg. respectively. As the equilibrium angles were not set crystal structure values, the minimized structure's parameters was more sensitive to force constant values than before. Therefore, the choice of force constants in the Sundar/Sontum_new modeling approach depended on both structural and vibrational fits. The units for the stretching and bending constants are kcal mol -1 A-2 and kcal mol-1 respectively.
Dihedral Parameters (Bond torsion)
These bond rotation terms restrict rotation around bonds. The potential energy of rotation around a bond is given by this Fourier series expansion around the equilibrium dihedral angle. In equation 2.1, Vn is the potential barrier to rotation in kcal Mol-1, n is the periodicity, [[phi]] the rotation away from the equilibrium angle, and [[gamma]] the equilibrium dihedral angle. An additional redundancy factor, m, was also included in the PARM input file, although this term is not explicitly seen in the above force-field equation. This additional term is included to allow direct comparison of the total barrier to rotation around a bond with values listed in the literature. The dihedral Fourier series expansion reduces to a single term around each dihedral for relatively simple rotational potentials; for a double bond this dihedral Fourier expansion reduces to a single 2 fold (n=2) term. For more complicated types of rotational potentials, like in ethylbenzene, a combination of these terms was required. Other molecular modeling packages, like Spartan, were used to determine the exact shape of the rotational potential. Fourier analysis was done to decompose this potential into its key components, and the important terms were input into the PARM input file.
To help maintain planarity in molecules another, "improper" torsion term was also defined. These terms raise the potential energy of the molecule, if the angle between two planes defined by four non-consecutive atoms is distorted away from its predefined, equilibrium value. As there exist a variety of plane definitions, which are possible between four non-consecutive atoms (Figure 2.2), these improper torsion terms need to be explicitly defined in the PREP module. Furthermore, as there is no consistent functional dependence between the distortion and the resultant rise in potential energy caused by these improper torsion terms, care was taken while different improper terms were compared. Usually scaling factors were used while converting between various impropers defined on the same four atoms. Maggie Zraly had calculated the relevant scaling factors for improper torsion parameters listed in the literature. 23 These scaling factors were used when improper torsion parameters listed in the literature needed to be used within the framework of the AMBER force field.
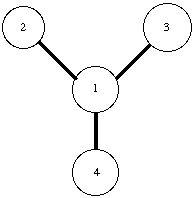
Figure 2.2 Different Improper Torsion Terms Possible on same Four Atoms
i. Angle defined by planes containing atoms 2, 1, &4 and 3, 1, & 4.
ii. Angle defined by planes containing atoms 2, 1, &3 and 4, 2, & 3.
These non-bonded parameters help to bring a molecule into its best spatial orientation. The physical effects represented by these parameters are Van der Waals and electrostatic forces. In AMBER 4.1, these parameters are defined between sets of atoms that are separated by at least 4 bonds. Steric interactions between atoms that 4 bond distances away are accounted for with this term.. As these parameters are sensitive to the net atomic charges, these charges needed to be carefully set. Usually, these charges were set to values obtained from semi-empirical calculations done in Spartan or values present in the standard AMBER 4.1 force field (parm94.dat). 25.
This module was designed to perform "molecular mechanics calculations on proteins and nucleic acids".25 In this thesis, this functionality has been extended to include other, much smaller molecules like benzene, ethylbenzene and the heme porphyrin. The NMODE module uses first and second derivative information to perform vibrational analyses of molecules around their equilibrium structure. 25 The vibrational frequencies are obtained by solving the Wilson-GF matrix composed of the various input force field constants. 17 The NMODE module writes out the x, y and z displacement vectors of the eigenvector solutions to the Wilson-GF matrix, along with the vibrational frequencies associated with these normal modes.
The NMANAL module was used to analyze the eigenvector data output from the NMODE module. These vectors were projected onto the various internal coordinates of the molecule, and the dependence of a particular eigenvector on these internal coordinates was determined. This dependence is known as the potential energy distribution (PED) of a particular mode or orbital, and provides an estimation of the "character" of a particular normal mode. If a mode of motion were comprised entirely of C-H stretches, then a large fraction of this mode's PED would contain contributions from C-H bond coordinates. Such a mode's character would then be classified as "primarily stretching" or "having significant stretching character". A sample script controlling both the NMODE as well as the NMANAL programs is listed in Appendix D.
The force field defined in the PARM module was optimized by comparing the normal mode frequencies generated by the NMODE module with experimentally observed frequencies. The various constants contained in the force field were changed, either by hand or using an algorithm, until the difference between the theoretically calculated and experimentally observed frequencies was minimized. Upon minimization of this difference, a consistent force field was said to have been obtained, as such a force field was consistent with experimentally observed data. The focus of this thesis was to generate a consistent force field for the NiOEP molecule. Transferability of this optimized force field was emphasized for two reasons: the NiOEP force field had to be transferred to the heme porphyrin; new approaches towards developing force fields needed to be tested on smaller molecules like benzene, toluene and ethylbenzene, and the results of such testing needed to be transferred over to the nickel porphyrin.
Fundamentally the Wilson-GF matrix in molecular mechanics is under-determined, as the total number of normal modes is smaller than the number of force constants present in the GF matrix. 15 It is possible to arrive at similar, optimized frequency matches with different force fields (i.e. different sets of force constants yield the same set of frequencies). There exists another problem which becomes acute as the size of the modeled molecule increases. For an N-atom molecule, the total number of normal modes is 3N-6. As these various modes span the same frequency range (approximately 3000 cm-1 in porphyrin systems), in bigger molecules it is difficult to assign and match correct normal modes to observed frequencies. This misalignment problem is particularly acute in the 400 cm-1 to 1100 cm-1 range, where dihedral, bending and stretching frequencies are found. While isotopic shift data and structural features of the modeled molecule helped to increase the criteria with which to select a particular force field, additional considerations were needed to help make correct matches between calculated and observed frequencies.
All the molecules, whose force fields were optimized, possessed inherent symmetry and belonged to a symmetry point group. Group theoretical considerations classify a molecule's normal modes into irreducible representations (symmetry types). Symmetry considerations preclude normal modes belonging to different irreducible representations from mixing . Therefore, optimization of the force field was done within each irreducible representation, where assignments of frequencies became easier. Additional algorithms were developed to combine the output from the NMANAL and NMODE modules with these symmetry considerations. A description of these algorithms follows.
Symmetry Program (nsym)
Normal modes belonging to the same symmetry type transform in the same fashion under individual, symmetry operations. Within an irreducible representation, the dot product of eigenvectors transformed by a symmetry operation with untransformed eigenvectors are the same. Normal modes that were symmetric and anti-symmetric with respect to the symmetry operation have dot product values of 1 and -1 respectively. Degenerate normal modes, on the other hand, have dot products that were 0, 1 nor -1. The dot products of four operations was exploited by the nsym algorithm, which classified various normal modes into their symmetry types. A 'syminfo' input file was created, in which matrices corresponding to four symmetry operations in the molecules point group were defined. The dot products of eigenvector transformation were then computed by the nsym algorithm. As the syminfo file also contained the expected dot products for each of the irreducible representations, the eigenvectors generated by the NMODE module could be classified by the nsym algorithm. The expected number of normal modes within each irreducible representation was also present in the input file. This input was used by the nsym module as a check. If there were problems in assigning the symmetry type, the nsym module calculated a flake index which quantified the difference between the actual and calculated dot products. The symmetry types of molecular vibrations which had high flake indices were reassigned in a random fashion until the number normal modes assigned to each symmetry type matched the input in the syminfo file. Serious problems in symmetry matches indicate imbalances in the force field itself, hence the symmetry criterion helped develop well-balanced force fields. The syminfo files used for the different molecules are listed in Appendix E.
Potential Energy Distribution (nfit algorithm)
Another criterion considered while making normal mode assignments was the "character" of the various vibrations. As mentioned before, the NMANAL module computes the sensitivity of the various normal modes to the internal coordinates (bonds etc.). This sensitivity is quantified by the NMANAL module as a percentage of the total potential energy of the normal mode. An algorithm was developed which used the PED data computed by the NMANAL module to determine the character of all the normal modes. If a normal mode were only dependent upon torsion coordinates, then it was given a character of 40. Similarly, pure bending and stretching normal modes were assigned characters of 30 and 20 respectively. Normal modes, in which different internal coordinates mixed, did not have pure 20, 30, or 40 character values, instead their characters were determined by the nfit algorithm as a weighted average of their PED values. Such classification of orbitals was done because literature data was often classified using PED distribution values. Therefore, in our observed files, experimentally observed data was also classified according to their characters. Normal modes which were pure dihedral, bend or stretch in character were assigned values of 40, 30 and 20 respectively. For orbitals that were mixed in their character, Table 2.1 list the classification that was used to separate out mixed character, observed frequencies.
Table 2.1 Character Classification Used.
Bond Character (=X) Associated Value Bond and Dihedral mix 15 < X < 20. Bond and Bend mix 20 < X < 30. Dihedral and Angle mix 30 < X < 40. Dihedral and Angle mix 40 < X < 45 .
Once the calculated normal modes had been classified according to their symmetry types and character, they were compiled into a file called the calc.file. In this file, the calculated frequencies were listed in increasing order of their frequencies, along with their irreducible representation (symmetry) and bond character (character). Finally, frequencies belonging to the same symmetry type were ranked in increasing order of their frequency (position). This ranking constituted the "position" of the normal modes. Classification and ordering of the frequencies within the calc.file became necessary to have a systematic method of comparing calculated and experimental frequencies.
Experimentally observed frequencies were listed in an observed file, in which the character, position and frequency of these observed frequencies were listed. As the format of the observed frequencies was similar to that of the calculated frequencies listed in the calc.file, it was possible to develop algorithms which matched calculated and observed normal modes.
The nfit_12 algorithm matched the various orbitals generated by the NMODE and classified by other modules and algorithms in the calc.file to those listed in an observed file. It made these assignments by comparing the symmetry, character, position and frequency of the calculated orbitals within the calc.file with those values specified in the observed file. This algorithm was set up such that it was possible to weight the relative importance of each of these factors (symmetry, character, position and frequency) while making the assignments. The formula used by this algorithm to determine the best possible assignment is given by Equation 2.2:
MATCH= {W1([[sigma]]obs-[[sigma]]calc) }2 + {W2([[tau]]obs-[[tau]]calc)}2+ {W3(Pcalc-Pobs)}2 + {W4([[upsilon]]calc-[[upsilon]]obs)} 2
Equation 2.2 Equation Used to Determine the Best Possible Orbital Match up.
In equation 2.2, w refers to weights for each of the individual match criteria. [[sigma]] represents the symmetry types of the observed and calculated frequencies being matched together. Similarly, [[tau]], P and [[upsilon]] refer to the character, position and frequency classifications of the observed and calculated frequencies. The nfit_12 algorithm used the MATCH equation to compare calculated and observed frequencies. All the frequencies were assigned so that the value of the MATCH equation was minimized. It was possible to control the types of matches being made by altering the weights associated with each individual match criteria. As group theoretical considerations do not allow mixing of normal modes between different symmetries, it became necessary to prevent the matching of observed and calculated frequencies belonging to different symmetries. Setting weights associated with the symmetry matches to values much larger than those associated with the character, position and frequency matches ensured that matching of orbitals between symmetries did not occur. Typically the following sets of weights were used: w1=300, w2=5.0, w3=1.0, w4=0. The weight associated with the frequencies of the orbitals (w4) was kept at zero, so that mixing of orbitals between symmetries was avoided when the force fields was not optimized.
The nfit_12 matching algorithm had several filters that could be applied to further control the type of assignments that occurred. One option was to allow "redundancy" matches between observed and calculated frequencies (ioption=0). Several calculated frequencies could be matched to a single observed frequency. Therefore, each calculated frequency was compared to all the observed frequencies to find the minimum value for the MATCH equation. Thus, matches could be completed even when the number of calculated orbitals with a particular character did not match the number of normal modes listed in the observed file. It was hoped that once the parameters were sufficiently optimized, the characters of the calculated orbitals would automatically correspond to those listed in the observed file. Another consistently used, matching option was the "lockout" match (ioption=1), which removed redundancies by locking out the calculated frequencies. Therefore, the observed set continually got smaller as the matches progressed. The problem with this option, however, was that if a misasignment occurred in the low lying frequencies, the error was carried forward to all subsequent matches also. To correct for this deficiency, another option was developed (ioption=2). This option contained an additional refinement. Once a frequency had been assigned with the lockout match (ioption=1), the remaining frequencies were reordered, from to low to high, before any further assignments were done. The nsymm algorithm with ioption=2 was mostly used, as this option consistently gave the best match.
While the nfit algorithm helped to classify the various vibration into bond, bend or dihedral characters, it did not provide any information regarding the actual dihedral, bend or stretch parameters that were involved with these orbitals. Two additional methods were developed to help visualize, or determine the "shape" of, the calculated orbitals.
The nmode_p module projected each of the atom eigenvectors for a particular normal mode on to the x-y plane. The value of this projection was then written out, and could be compared to eigenvector diagrams determined by Spiro's group for the nickel porphyrins. This module proved to be adequate in visualizing pure "out of plane" (OOP) motions of normal modes, but inplane motions could not be tracked by this module. Another program was developed to look at the 3 dimensional shapes of the various normal modes.
The Run.vis script subtracted a certain proportion of an normal mode eigenvector, produced by the NMODE module, from the equilibrium position of the atoms. The resultant difference was then written out in a PDB format along with the equilibrium positions of the atoms. A superimposed figure was then obtained by visualizing the output PDB file using RASMOL. Thus, the 3-dimensional displacement occurring in a particular normal mode was visualized. Figures 2.3 and 2.4 show the sample visualization of normal modes, as seen using the run_p and Run.vis scripts.
............................................................
. -3 2 .
. -1 42 .
. -1 1 .
. -1 -1 1 0 .
. -1 0 .
. 0 0 .
. .
. 2 -3 .
. 1 0 -1 -1 .
. 7 6 1 -2 -5-7 .
. 1 0 -1 .
. -2 0 3 .
. -9 2 -2 10 .
. 2 -2 .
. 2 0 -2 .
. 2 -2 .
. -10 2 -2 9 .
. -30 0 2 .
. 1 0 -1 .
. 7 5 2 -1 -6 7 .
. 1 1 0 -1 .
. 3 -2 .
. .
. 0 0 .
. 0 1 .
. 0 -1 1 1 .
. -1 1 .
. --4 1 .
. -2 3 .
............................................................
Figure 2.3 Run_p output for OOP mode Vibration
Numbers refer to Eigenvector Projections on the xy plane.
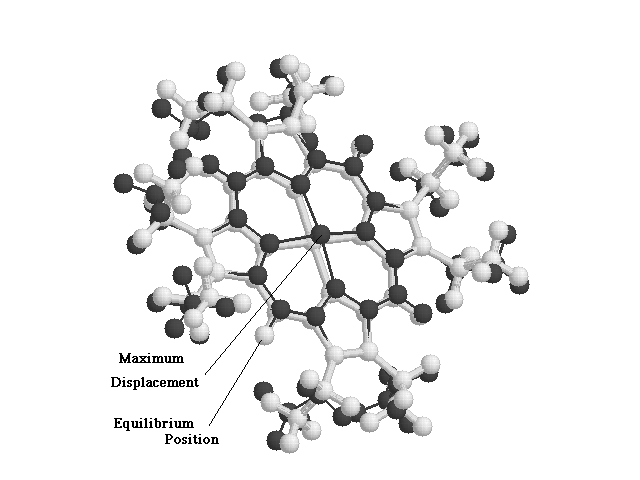 Figure
2.4 Run.vis Output for an O.O.P. Normal Mode.
Figure
2.4 Run.vis Output for an O.O.P. Normal Mode.
Light trace represents the NiOEP Molecule at its Equilibrium Position.
Dark Trace shows the NiOEP molecule at Maximum Displacement in this particular Normal Mode.
A non-linear, weighted optimization procedure was used to improve the correlation between calculated and observed frequencies, once these two sets of frequencies were matched correctly using the MATCH equation. The following formula was used to determine correlation between correctly assigned frequencies.
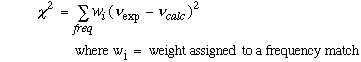
Equation 2.3 Average Weighted Standard Deviation Equation.
The weights were usually assigned depending on the accuracy of the observed
frequency. The weights were calculated using the formula
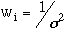 ,
where
,
where
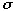 was the uncertainty in the observed frequency. Some of the frequencies listed
by Li et. al, were not observed by them, but rather predicted by their own
vibrational force field. Therefore, while these frequencies were listed in the
observed file, the weights associated with these frequencies was set to zero.
While some degree of "hand-tweaking" of the various force constants was done,
to get the order of these frequencies to approximately match the observed
frequencies, coupling between parameters prevented extensive use of this
method. Therefore, two algorithms were developed, which did such
"hand-tweaking" in a controlled, iterative fashion.
was the uncertainty in the observed frequency. Some of the frequencies listed
by Li et. al, were not observed by them, but rather predicted by their own
vibrational force field. Therefore, while these frequencies were listed in the
observed file, the weights associated with these frequencies was set to zero.
While some degree of "hand-tweaking" of the various force constants was done,
to get the order of these frequencies to approximately match the observed
frequencies, coupling between parameters prevented extensive use of this
method. Therefore, two algorithms were developed, which did such
"hand-tweaking" in a controlled, iterative fashion.
This algorithm 28 allowed systematic variation of sets of parameters, in a manner that reduces the [[chi]]2. As the name suggest this algorithm runs on a [[chi]]2contour map and connects the "ravines" which exist in this map. It steps along the largest gradient on the contour map to reduce the [[chi]]2. A central assumption made when using this technique is that the various valleys in the [[chi]]2 contour map are interconnected. In the event that these ravines were not interconnected, the algorithm was started from different positions on the contour map (different values for the parm sets) in the hope that all minimum value contours would be located.
While the ravine algorithm located the different local minima present in the [[chi]]2 contour, a more sophisticated algorithm 29 was required to locate the absolute minima within each of these valleys. This requirement was satisfied with the simplex algorithm. The disadvantage of this method, however, was that it was capable of locating the absolute minima only within a single valley. Therefore, a combination of the ravine and simplex algorithms were used to search for global [[chi]]2 minima.
Once many such minima had been located from different starting points in the [[chi]]2 space, the physical viability of the force fields responsible for each of the [[chi]]2 minima was considered. The shapes of the calculated orbitals were visualized using either the run_p or run.vis programs. Consistency in the shapes between the calculated and observed frequencies was sought, and hence some optimized force fields were excluded. Structural features of the molecule, upon application of the optimized force-field were analyzed. If an optimized and consistent force field were the truly the best one possible, it should reproduce experimentally observed vibrational modes and structural features of that molecule. This stringent, evaluation criteria allowed us to discard various optimized parameter sets in favor of one, more general parameter set for the NiOEP molecule. Lastly, force fields which displayed intuitive consistency and trends between the values of the various parameters were favored. The final force field selected for the NiOEP molecule satisfies all these requirements and proved to be transferable over to the heme porphyrin. The optimized heme porphyrin force field was placed in different environments to see if this force field could reproduce the structural features of the heme residue in different environments. The final optimized force fields are listed in Appendix F.
In order to analyze the effects of the protein environment on the normal modes of the carboxyheme, it was necessary to freeze out the movements of the rest of the protein. By freezing out the movements of the protein, it should be possible to concentrate our frequency analysis on the carboxyheme segment, while at the same time taking into account the steric and electronic effects of the rest of the protein on the porphyrin normal modes. Freezing out of the rest of the protein would have been done by using the "belly" option provided in the AMBER package. However, glitches in the operation of this option, particularly in the nmode module, prevented the use of this function. Therefore, no analysis was possible inside the protein.
Chapter 3- Results Small Molecules
The primary goal of this project was to develop and utilize a consistent force field for heme porphyrins. As we started this development with nickel porphyrins, a requirement of transferability was imposed on all optimized force fields, so that the eventual transfer of nickel porphyrin force fields to heme would be simple.
Jason Dimmig had completed the optimization of a transferable force field which accurately simulated the inplane motions of nickel porphyrin (NiP) using a united ethyl approximation of nickel octaethyl porphyrin (NiOEPz). 24 Figure 3.1 shows the simplification made by Dimmig.
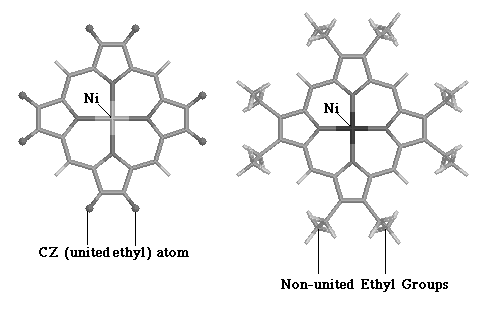 Figure
3.1 Comparison of Structural Features Between NiOEPz and NiOEP.
Figure
3.1 Comparison of Structural Features Between NiOEPz and NiOEP.
As figure 3.1 shows, the ethyl groups at the periphery of the NiOEP were assumed to be single point masses in the NiEOPz model, with a combined mass of 29 amu. This approximation allowed two simplifications: the NiOEPz molecule was planar and hence the out-of-plane (OOP) and inplane (IP) modes were decoupled; and, the number vibrational frequencies being modeled was reduced from 255 to 111. Dimmig succeeded in optimizing IP parameters (bond stretch and angle bend) of the porphyrin core and attempted to complete such optimization for the out-of-plane parameters. Complete optimization, however, was not possible because of the united ethyl approximation made in the NiOEPz model. Jason Dimmig states in his thesis, " our biggest problem with the CZ atom seems to be that we are optimizing on full ethyl observed data with a united ethyl atom." 24 All modes associated with the internal motions of the ethyl group, could not be simulated by united ethyl atoms. The immediate focus in this thesis was to complete development of the NiOEP force field, after having relaxed the united atom approximation made in Jason Dimmig's thesis. The transferable force field developed by Jason Dimmig 24 was used as a starting point for the optimization procedure.
Relaxation of United Ethyl Approximation
Our strategy was to relax the united ethyl approximation in a step-wise fashion i.e. first move to a united methyl-methylene (NiOEPx), then to a united methyl-non-united methylene (NiOEPy) used in Li's force field development, and finally to a fully non-united ethyl atom (NiOEP) (Figure 3.2).

Figure 3.2 Step-wise Relaxation of United Ethyl Approximation
While each of the models shown in Figure 3.2 (NiOEPz, NiOEPx and NiOEPy) were useful as approximations, the problems arising from the oversimplification of the ethyl groups persisted. Specifically, internal ethyl group vibrations were not calculated in the correct frequency range. Reasons for such poor correlation became apparent when simulations were performed on other computation packages. One set of simulations done on ethylbenzene using Spartan suggested strong coupling between the vibrations of methyl and methylene hydrogens. Additionally, Kincaid et. al. point out the coupling between the vibrations of ethyl group hydrogen atoms in porphyrin systems. 30 None of the approximate models (NiOEPz, NiOEPx and NiOEPy) include the methyl hydrogens, which can couple in the required fashion. Existence of such coupling prompted complete relaxation of the united ethyl approximation, and optimizations on NiOEP were attempted.
Non-United Nickel Octaethyl Porphyrin
Optimization of the full NiOEP force field proved difficult, because of the increased numbers of normal modes (255). These difficulties were circumvented by analyzing a smaller molecule, ethylbenzene, which contained an ethyl group at the periphery of an aromatic ring. Figure 3.3 displays the similarities between ethylbenzene and NiOEP.
Figure 3.3
 Figure
3.3 Structural Similarities between NiOEP and Ethylbenzene
Figure
3.3 Structural Similarities between NiOEP and Ethylbenzene
As our main interest in smaller molecules was to develop a force-field which reproduced the vibration frequencies of an ethyl group connected to an aromatic ring. Figure 3.3 demonstrates the suitability of ethylbenzene. This molecule also has an ethyl group attached to an aromatic ring, much like NiOEP itself, and allows easier understanding of force field requirements for modeling the ethyl group. Additionally, the smaller number of vibration frequencies in ethylbenzene allowed us to test out different modeling approaches, before selecting a method to use in NiOEP. The results of such analysis will be described in the following sections.
Force Field Development for Benzene, Toluene and Ethylbenzene.
Before ethylbenzene could be modeled, existing force fields for benzene and toluene needed to be revised. The standard AMBER force fields for both these molecules produced poor vibrational fits, which in turn, caused poor vibrational fits for ethylbenzene. The existing force fields for benzene and toluene were corrected, and information extracted from such corrections gave us a clearer insight into the nature of the OOP parameters used in the AMBER force field. These conclusions are discussed in the next few sections.
Benzene
As mentioned before, the standard AMBER force field produced a poor vibrational fit. When the calculated frequencies were analyzed using the NMANAL, run_p and run.vis programs, it became apparent that the primary problems were in the OOP modes of vibrations. The philosophy of Kollman et al. in modeling the OOP modes of benzene was to simplify the parameters required as much as possible. 18 Dihedral terms were defined with wild cards, so that a single dihedral term would suffice for all the dihedral definitions around a bond. Such emphasis on simplicity affected the accuracy of the benzene force field. As a correction we developed a new force field for benzene in which dihedrals were specifically defined. Figure 3.4 illustrates the nature of the change effected in the standard AMBER dihedral parameters.
 Figure
3.4 OOP Force Field Parameters in the Standard AMBER and New Parameter
Sets
Figure
3.4 OOP Force Field Parameters in the Standard AMBER and New Parameter
Sets
Our force field for benzene contained specific definitions for proper dihedrals in that we broke the standard X-CA-CA-X dihedral of AMBER into CA-CA-CA-CA, HA-CA-CA-CA and HA-CA-CA-HA. When the dihedral terms were not grouped, we noticed that good vibrational fit were possible without improper terms. This trend will be discussed separately in a future section of this chapter. The improved frequency correlation arising from this change is listed in Table 3.1, in which fits obtained with the new force field are contrasted with ones obtained with the standard AMBER force field.
Table 3.1 Frequencies Calculated from New and Standard AMBER Force Fields.
Symmetry Observed New Force Difference AMBER Difference
type Frequency Field (%) Force (%)
(cm-1) Frequency Field
(cm-1) (cm-1)
[[chi]]2 1384.3 4879.8
a2u 673.0 688.7 2.3 % 700.7 4.1%
b2g 703.0 686.3 2.3% 663.3 5.6
eu 995.0 996.2 0.1% 1195.6 20.1
b2u 1329.0 1666.6 25.4% 1729.0 30.1%
Improvements to the standard force field are evident from the [[chi]]2
values listed in Table 3.1, which have fallen from 4879.8 to 1384.3.
Focusing on the calculated differences, it is apparent that the correlation has
improved across the symmetries. The a2u, b2g and e2u symmetry frequencies are
all OOP modes of vibration, so improvements in these frequencies supports the
use of the more detailed OOP parameter set. The b2u symmetry observed
frequency at 1329 cm-1 is an IP frequency (Kekule Mode), which could
not be modeled by either of parameter sets. The poor correlation in this
frequency reflects an inherent deficiency in the AMBER potential equation (Eq.
2.1), in which off diagonal terms from the force matrix are incompletely
represented. This frequency was therefore excluded from all [[chi]]2
calculations. Further analysis of the specific dihedral terms offers a reason for the improved correlation in OOP mode frequencies. Table 3.2 tabulates the dihedral parameters defined in the new benzene force field and compares them to values listed in the standard benzene force field.
Table 3.2 Torsion Parameters Comparison.
Proper Dihedral Used New Force Field Standard Force
(kcal/ mol) Field (Kcal/ mol)
CA-CA-CA-CA (1) 4.178 N.A.
CA-CA-CA-HA (2) 8.063 N.A
HA-CA-CA-HA (1) 2.292 N.A
X -CA-CA-X (4) N.A 14.50
Improper Dihedrals Used
X- X- CA- HA 0.000 1.100
Total 14.542 15.474*
Values in ( ) refer to the redundancy factor (m) around the central bond
* Total contains scaled contribution from IMPROPER terms
As Table 3.2 shows, the sum of the specific dihedrals (14.542 kcal/ mol) defined in our new force field is similar to that in the standard force field (15.474 kcal/ mol). Such consistency is reassuring, because the total potential barrier around a bond should be independent of the internal distribution of such a barrier. Therefore, by breaking away from the general dihedral restriction employed in the standard AMBER force field, we have introduced more flexibility into our force field. This flexibility, in turn, is reflected in better vibrational fits for the OOP modes.
Before the benzene force field was transferred over to toluene, it transferability was tested on deuterated benzene. The physical effects of deuteration were simulated by changing the mass of the hydrogen atom within the force field from one to two amu, and by optimizing on the parameters that controlled the vibrations of the deuterium atom. Table 3.3 shows the vibrational fit for some samples normal modes using the AMBER and new force fields.
Table 3.3 Sample Frequencies Calculated Using the New and Standard AMBER Force Fields
Symmetry New Force Field AMBER Force Field Observed
(cm-1) (cm-1) Frequency
(cm-1) 31
31 [[chi]]2 807.9 2716.7
a2u 499.8 514.5 497.0
b2g 582.4 584.8 599.0
eu 820.8 959.3 830.0
b2u 1647.7 1705.4 1282.0
[[chi]]2 807.9 2716.7
a2u 499.8 514.5 497.0
b2g 582.4 584.8 599.0
eu 820.8 959.3 830.0
b2u 1647.7 1705.4 1282.0
The improvements made to the standard AMBER benzene parameter set are evident in this table, as the [[chi]]2 value for the fit has decreased from 2716.7 to 807.9. Furthermore, the improvements in correlation have happened in the same symmetry as in benzene, supporting our break from general dihedral definitions. Examining Table 3.3 reveals that the b2u frequency is modeled incorrectly, again highlighting the inherent deficiency in the AMBER force field equation mentioned in the previous section. Maintaining consistency with the approach used in the previous section, this b2u frequency was not included in any [[chi]]2 calculations.
Attempts to transfer the entire, newly-optimized benzene force field to toluene met with repeated failure. Further investigation revealed that this lack of transferability between the sets was concentrated around the apex carbon atom. While the entire toluene PREP file is listed in Appendix A, changes made to atom labels are summarized in figure 3.5.
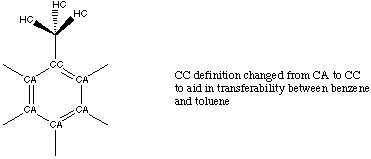
Figure 3.5 Atom Definitions Used in Toluene.
Once the apex carbon atom of the phenyl ring shown in figure 3.5 was redefined as CC, we were able to transfer parameters developed for the benzene CA atoms over to the remaining CA atoms in the phenyl ring of toluene. Additionally, we continued with the use of specific dihedral definitions to describe parameters containing the CC atom. Good vibrational fits could then be obtained by optimizing only the CC and methyl parameters. Table 3.4 compares the vibration fits obtained using our optimized and the standard AMBER force fields.
Table 3.4 Frequencies Calculated for Toluene using New and Standard AMBER Force Fields.
Symmetry Observed New Force Difference AMBER Difference
Frequencies Field (%) Force (%)
32
Field (%) Force (%)
32 (cm-1) Frequencie Field
s (cm-1) (cm-1)
[[chi]]2 1214 7418
a1 220.0 214.5 2.5% 222.3 1.0%
467.0 474.8 1.5% 455.6 2.4%
a2 44.0 43.5 1.1% 34.9 20.6%
348.0 365.7 4.8% 405.5 16.5%
(cm-1) Frequencie Field
s (cm-1) (cm-1)
[[chi]]2 1214 7418
a1 220.0 214.5 2.5% 222.3 1.0%
467.0 474.8 1.5% 455.6 2.4%
a2 44.0 43.5 1.1% 34.9 20.6%
348.0 365.7 4.8% 405.5 16.5%
Table 3.4 summarizes the improvements made with the new force field ([[chi]]2 value has fallen from 7418 to 1214). The high [[chi]]2 value with the standard AMBER force field reflects the inherent non-transferability of benzene parameters over to the apex carbon atom, and the poor vibration fits for the lower lying frequencies in the a2 symmetry. The improvement matches in the low lying frequencies again supports the break in dihedral parameters employed in our new force field. Once again, while no improper terms were required for the CA atoms, one was needed around the CC atom. This interesting exception will be revisited later in this chapter.
Our success in transferring most of the benzene force field over to toluene, encouraged us to transfer the toluene force field over to ethylbenzene. Although optimizing the ethylbenzene force field with an additional atom should have been easy, especially with the new CC atom definition employed in toluene's force field, considerable difficulties were encountered in trying to optimize the low lying frequencies. Table 3.5 lists two low lying frequencies, both of which could not be optimized simultaneously.
Table 3.5 Calculated and Observed Low Lying Frequencies in Ethylbenzene.
Symmetry Observed Calculated a1 150.7 152.0 a2 45.0 115.9
Analysis of the two frequencies listed in Table 3.5 revealed that they depended on the same parameter (CA-CC-CT-CT). It was not possible to reduce the CA-CC-CT-CT dihedral and improve the a2 frequency match, without worsening the a1 match. Visualization of both these orbitals revealed that they were dependent on the rotation of the ethyl group attached to the phenyl ring. We found that improvements to this fit were possible if an additional term was included in the proper torsion Fourier expansion of the AMBER force field equation (equation 2.1). Specifically, an additional, fourth order term (n=4) term had to be employed around the CA-CC-CT-CT dihedral. Table 3.6 lists the fit of these low lying frequencies once the fourth order term had been included. This vibrational fit has been compared to the fit obtained without the inclusion of the fourth order dihedral potential term.
Table 3.6 Ethyl Group Frequencies With and Without the Inclusion of the fourth Order Fourier Expansion.
Symmetry fourth Order Term fourth Order Term Observed
Included (cm-1) Excluded (cm-1) Frequency
(cm-1) 32
32 a1 148.2 152.0 150.7
a2 48.7 115.8 45.0
a1 148.2 152.0 150.7
a2 48.7 115.8 45.0
Table 3.6 displays the importance of including the fourth order potential term
to model the rotation barrier of the ethyl group, when this group is attached
to benzene (an aromatic molecule). The fourth order affects the a2 term more
significantly than the a1 term, and, counter intuitively, causes the a2
frequency to decrease. Both these changes, however, improve the
correlation between calculated and observed frequencies. It is important to
understand the underlying reasons for such an improvement, especially because
NiOEP also has ethyl groups attached to an aromatic ring. Conclusions regarding
the rotation of the ethyl group in ethylbenzene should be applicable in the
case of NiOEP as well. Investigation of literature 33 and abinitio calculations done using Spartan yielded an explanation for the additional dihedral term that is required. Figure 3.6 shows the rotational potential seen for ethylbenzene around the CC-CT bond, as calculated by Spartan.

Figure 3.6 Rotational Potential in Ethylbenzene.
While at first glance the rotational potential around the CC-CT bond in figure 3.6 may look like a simple two fold potential (n=2 in dihedral expansion), closer inspection reveals that the maxima of this curve does not resemble the corresponding minima. Additional Fourier analysis of this potential barrier (also shown in figure 3.6) reveals that this term was composed of two distinct rotational potentials- a dominant two fold and a minor four fold term. In the standard AMBER force field, 18 only a two fold term is used to model the ethylbenzene rotation barrier, explaining the inability of this force field to reproduce the low-lying orbitals correctly.
The coefficients obtained from this analysis were used as starting Vn values. Optimization of the expanded set of dihedral terms was then done using ravine and simplex algorithms, until the frequency matches were improved. Table 3.7 compares the theoretically calculated and final torsion potential values that were used.
Table 3.7 Comparison of Spartan Calculated and Optimized Torsion Parameter Values
Parameter Type Calculated Final Potential
Barrier (kcal/Mol) (Vn) Values used.
(Kcal/mol)
n=4 0.284 0.560
n=2 2.258 2.308
Table 3.7 indicates that while the final second order dihedral term used
corresponds to those calculated by Spartan, the optimized fourth order term is
almost double the Spartan calculated value. One possible reason, for such a
trend is the existence of other, higher order dihedral terms which describe
this rotational parameter. The magnitudes of these terms are small, but maybe
the fourth order term is compensating for these absent higher order terms.
Therefore, as long as higher order Fourier expansion terms are present,
barriers calculated by Spartan seem to be transferable to the AMBER potential
set.
As indicated consistently during the discussions of proper dihedral parameters earlier in this chapter, an interesting observation concerning the use of improper terms was made. These observations are now summarized and trends extracted from such a summary.
As mentioned in chapter two, improper terms help maintain the planarity of molecules. However, there is no consistent functional dependence between perturbations and the rise in potential energy caused by improper torsion terms. As a result, when literature values of improper terms are compared, their values have to be scaled by different scaling factors before they can be used within the AMBER framework.
Our observation concerns the need to use these improper terms. In our analysis of benzene and its deuterated analog, toluene and ethylbenzene, we found that an improper term was needed only in toluene and ethylbenzene, and furthermore, this improper was required only around the CC atom. In the case of benzene such impropers were not required. It seems like the excluded improper terms around CA atoms are compensated for by the extended proper dihedral set. Table 3.8 lists the optimized frequency fits possible in ethylbenzene and toluene with and without the use of the CC improper term.
Table 3.8 Effects of Using Improper Term Defined Around CC Atom in Toluene and Ethylbenzene
Optimized Force Field Optimized Force Field
with CC Improper without CC Improper
[[chi]]2 (Toluene) 1214.0 1485.3
[[chi]]2 (Ethyl benzene) 851.3 929.8
The higher [[chi]]2 values in table 3.8 shows the need for improper terms around the CC atom. An additional F-series test confirmed that the fall in [[chi]]2 value was statistically significant at the 90% level. One possible reason for this could be understood by considering the CC atom and the CC-CT bond in toluene and ethylbenzene.
Clearly, the CC atom is not like the rest of the CA atoms in the phenyl ring. This is evidenced by the fact that CA parameters (from benzene) do not yield good vibrational fits when transferred over to this CC atom. Additionally, the CC-CT bond in both ethylbenzene and toluene is a single bond, which could hyperconjugate with the CT-HC bond (Figure 3.7). The resulting partial double bond character of this bond is not modeled by any of the other terms present in the AMBER force field equation. Therefore, it is possible that improper terms are required to represent hyperconjugation effects within the AMBER force field.
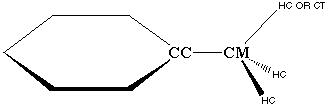
Figure 3.7 Possible Hyper conjugation Between CC-CM Bond and CM-HC bonds
Conclusion Transferred over to NiOEP.
Our modeling of ethylbenzene in its entirety has enabled us to probe and better understand the nature of OOP parameters. Conclusions derived from such analysis were used while modeling NiOEP's OOP parameters. Important conclusions that were transferred include the following. Just as in benzene, dihedral definitions were made more specific and improper terms were excluded unless hyperconjugation were possible. A fourth order dihedral term was included to describe the rotation of the ethyl group. Finally, the parameters developed for the ethyl group were used as a starting point for optimizing ethyl group parameters in NiOEP.
Chapter 4- Results Old Force Field
After obtaining a good potential set for the ethyl group, a consistent force field for NiOEP (Sundar/Sontum_old) was developed by transferring these ethyl group parameters over to the averaged, transferable porphyrin force field developed by Jason Dimmig. Thereafter, another consistent force field (Sundar/Sontum_new) was also sucessfully developed. Each of these force fields result from the fundamentally different modeling approaches described in the methods section. The feasibility of each of the force fields was then evaluated against the criteria mentioned at the end of the methods section. While both of these force fields satisfy these requirements, the Sundar/Sontum_new force field is intuitively more appealing and hence favored. The force field developed first (Sundar/Sontum_old) is evaluated in this chapter. Examination of the Sundar/Sontum_new force field is left for the nextchapter.
The most important requirement of the Sundar/Sontum_old force field was that it reproduce the vibrational features of NiOEP. As the Sundar/Sontum_old force field is vibrationally consistent, its optimized parameters were compared to other porphyrin force fields, in order to evaluate the feasibility of these optimized parameters. Such a comparison is done in Table 4.1, where bond force constants in the Sundar/Sontum_old, united ethyl Dimmig/ Sontum and three other force fields are compared.
Table 4.1 Bond Force Constants for NiOEP
Sundar/ Dimmig/ Spiro 19-21, Karplus
19-21, Karplus 34
34 AMBER
AMBER 18
18 Sontum Old Sontum 33
Sontum Old Sontum 33 (Averaged)
[[chi]]2 1656. 1537. 5840. 2684. 7288.
BONDS
NI-NP 157.246 145.000 121.000 270.200 50.000
NP-CC 297.322 313.538 427.500 377.200 428.00
CC-CB 260.679 287.400 391.000 299.800 416.000
CC-CD 327.507 361.863 502.000 360.000 500.000
CB-CB 413.607 426.790 512.000 340.700 546.000
CD-HM 356.507 361.107 361.000 367.600 367.000
CB-CX 282.851 410.766* 302.300 441.300 317.000
CX-CY 329.418 N.A. 331.000 441.300 310.000
CX-HE 337.442 N.A. 328.000 367.000 340.000
CY-HN 337.442 N.A. N.A. 367.000 340.000
(Averaged)
[[chi]]2 1656. 1537. 5840. 2684. 7288.
BONDS
NI-NP 157.246 145.000 121.000 270.200 50.000
NP-CC 297.322 313.538 427.500 377.200 428.00
CC-CB 260.679 287.400 391.000 299.800 416.000
CC-CD 327.507 361.863 502.000 360.000 500.000
CB-CB 413.607 426.790 512.000 340.700 546.000
CD-HM 356.507 361.107 361.000 367.600 367.000
CB-CX 282.851 410.766* 302.300 441.300 317.000
CX-CY 329.418 N.A. 331.000 441.300 310.000
CX-HE 337.442 N.A. 328.000 367.000 340.000
CY-HN 337.442 N.A. N.A. 367.000 340.000
The [[chi]]2 values listed in Table 4.1 represent the fit each of
individual force field when used in the AMBER force field package. Several
approximations were made while evaluating the Spiro, Karplus and AMBER force
fields. Firstly, the Spiro force field listed here does not include the
non-transferable, off-diagonal terms used by the actual Spiro vibrational force
field. Additionally, as the Spiro force field was developed for a united
methyl model (NiOEPy in our naming scheme), internal methyl group parameters
(CY-HN) were approximated from the standard AMBER force field. The Karplus and
AMBER force fields were developed for the heme porphryin, so the Ni-N constant
listed under each of these force fields is the Fe-N constant transferred from
protoporphyrin IX, and ethyl group parameters are approximated with standard
AMBER values.Our goal was to improve the force constants listed in the standard AMBER force field, so that vibrations of porphyrin systems are better simulated. As Table 4.1 shows this goal has been achieved. The [[chi]]2 for the Sundar/Sontum_old is only higher than that of the Dimmig/Sontum force field. Even in this case, however, the frequency and character fits of the low lying frequencies is better. Therefore, even with a higher [[chi]]2 value, the Sundar/Sontum_old force field gives better vibrational fits. Furthermore, the average root mean square (rms) error of our force field, 40.69 cm-1, is, we believe, the lowest error limit possible using the AMBER force field equation. Actually, any rms values around 40 cm-1 is believed to be at the lower limits of the AMBER force field for the following reasons. Kollman et al. in their papers are content with AMBER force fields which have root mean square errors of 40. 18 Even in our own investigations of smaller molecules like toluene and ethylbenzene, our best optimized force fields had rms errors in the 40 cm-1 range.
Not surprisingly, the correlation between parameters and [[chi]]2 values in the Sundar/ Sontum and Dimmig/Sontum force fields is the best. The similarity of these values reflects the inherent transferability of both the force fields. No ethyl group parameters had been developed by Dimmig, therefore, standard AMBER values were used instead.
If the Dimmig/Sontum force field is excluded, then the Sundar/ Sontum_old force field matches up best with the Karplus force field. Our Ni-N constant is 42% smaller, while our CB-CB force constant is 18% larger. These trends are similar to those observed by Dimmig in his thesis, reinforcing the transferability of that united atom force field to the Sundar/Sontum_old force field. The ethyl group parameters do not match up between the Sundar/Sontum_old and Karplus force fields. Karplus' force field has both the CX-CY and CB-CX constants set to 441 kcal/mol, which although higher than values used in the Spiro and AMBER force fields, match the optimized constants in the Dimmig/Sontum united ethyl model. We believe that Karplus did not develop parameters for the ethyl group, but chose instead to transfer united ethyl parameters.
Various attributes of each of the listed force field become apparent, when Table 4.1 is examined closer. For example, the simplicity of the standard, AMBER force field is appealing. Fundamentally, the development of AMBER bond force constants was done by "linear interpolation between pure single and double bond values using the observed bond distances." 18 The result of such a modeling philosophy is the correspondence seen between bond orders and force constants. As a result, the CB-CB bond (bond order= 1.75) has the largest constant (546.0 kcal/ Mol-1), while the CX-CY bond (bond order=1.0) has the lowest force constant (310.0 kcal/ Mol-1). The problem with the standard force field, however, is the poor vibrational fit it gives when used to describe the vibrational frequencies of the NiOEP. The high [[chi]]2 value obtained with the standard force field indicates the "poorness" of the vibrational fit.
Lastly, as mentioned before, comparison of the Spiro force field within the AMBER framework cannot be done effectively . Spiro's vibrational force field had interaction constants, which do not have an analog within the AMBER force field philosophy. While non-bonded terms attempt to simulate off-diagonals terms, there is no simple, direct relationship between non-bonded and off-diagonal terms. Not surprisingly, high [[chi]]2 values result when the Spiro force field is placed within our AMBER force field framework, reflecting the inherrent non-transferability of this force field.
The range seen in literature for the nickel-nitrogen constant (Ni-N) is from 50 to 270 kcal/ mol. Dimmig determined that the range of force constants for this parameter in his model was between 120 and 280 kcal/mol. 24 However, no convincing reason could be developed for setting the value of this constant at 145 kcal/ Mol. We experienced a similar problem with our force field. The range of values that the Sundar/Sontum_force field allows for the Ni-N force contast in between 120 and 280 kcal/ Mol. A choice of 157 kcal/ Mol was made by final optimization of the force field, once the values for all the other parameters had been chosen. Resolution of the nickel-nitrogen force constant ambiguity led to the development of Sundar/Sontum_new force field, and so this ambiguity is reconsidered in the next chapter.
The other set of inplane parameters directly transferred from Dimmig's optimized united atom model were the angle bending constants. Table 4.2 lists the angle constants from the four force fields listed in Table 4.1. Again, the transferable Dimmig/ Sontum force field was the starting point in the development of the Sundar/Sontum_old force field.
Table 4.2 Angle Force Constants
Sundar/ Dimmig/ Spiro Karplus AMBER
Sontum_old Sontum
(Averaged)
ANGLES
NP-NI-NP 0.000 0.000 0.000 0.000 0.000
NO-NI-NP 8.780 29.454 18.000 50.000 0.000
NI-NP-CC 87.705 64.740 22.000 96.150 0.000
NP-CC-CB 117.615 121.926 99.000 122.00 70.000
NP-CC-CD 36.191 27.753 60.000 88.000 70.000
CB-CC-CD 36.191 27.753 60.000 61.600 70.000
CC-NP-CC 130.413 127.505 117.00 139.300 70.000
CC-CB-CB 90.796 60.050 99.000 30.080 70.000
CC-CD-CC 166.070 157.490 79.000 94.200 70.000
CC-CD-HM 32.014 29.167 36.000 12.700 35.000
CC-CB-CX 29.230 76.366 86.000 65.000 70.000
CB-CB-CX 29.230 76.366 56.000 65.000 70.000
CB-CX-CY 93.004 N.A. 54.000 70.000 70.000
CB-CX-HE 55.062 N.A. 45.000 50.000
CX-CY-HE 35.847 N.A. N.A. N.A. 50.000
CY-CX-HE 35.847 N.A. 45.000 N.A. 50.000
HE-CX-HE 31.560 N.A. 39.000 N.A. 35.000
HN-CY-HN 31.560 N.A. N.A. N.A. 35.000
*Listed
force constants have units of Kcal / mol. The same approximations mentioned in the discussion of the bond parameters were made with these force field parameters also. As table 4.2 shows, the Sundar/ Sontum angle bending constants closely correspond to the Dimmig/ Sontum force field, supporting the inherent transferability of these two force fields. As expected, force constants concerning the ethyl groups do not correspond between these two force fields as they represent different groups(united atom vs. non-united ethyl group). In the Sundar/Sontum_old force field, values for these ethyl parameters were transferred over from ethylbenzene and the optimized. Such additional optimization did not change the values of these ethyl group parameters by much, reinforcing the transferability of the ethylbenzene force field.
As seen in Dimmig's thesis, the CC-CD-CC constants value is much higher than corresponding values in other force fields. Also N-CC-CD and CB-CC-CD angle constants are much smaller than those listed in the Spiro, Karplus and AMBER force fields. Dimmig suggested that such a trend was indicative a trade-off between the CC-CD-CC parameter and the N-CC-CD/ CB-CC-CD set of parameters. These arguments seem to be valid in the Sundar/Sontum_old force field as well. While such an explanation seems reasonable, wide fluctuations in angle constants are avoided with the Sundar/Sontum_new force field. Another possible explanation for the observed fluctuations in the angle force constant will be offered in the next chapter, when the Sundar/Sontum_new force field is compared to the Sundar/Sontum_old force field.
Again, the simplicity of the AMBER force field is appealing. Unlike the other four force fields, bending constants within the standard AMBER force field do not vary by much. AMBER philosophy emphasises simplicity in force field development, Hence force constants in the standard, AMBER force field are 70, 50 or 30 kcal/ mol. The chief deficiency of the standard force field, however, is the poor vibrational fit to NiOEP is poor as indicated by the high [[chi]]2 value. The Sundar/Sontum_new force field will be shown to represent a compromise between the Dimmig/Sontum and AMBER force fields; retaining some of the AMBER simplicity, while still producing good vibrational fits.
Apart from a good vibrational fit, it was necessary that force field parameters (bond and angle constants) also gave a good structural fit for the porphyrin molecule. Dimmig et. al. determined that such a fit was best possible if the porphyrin had some strain built into it. Accordingly, the equilibrium bond (req in equation 2.1) and angle ([[theta]]eq in equation 2.1) were not taken from the crystal structure of NiOEP. The final equilibrium angles used by Dimmig for the CC-CD-CC and CC-N-CC values were set so that the minimized structure of NiOEP reproduced the same bond distances and angles like the crystal structure. According to Dimmig, "the strained set was found to be easily transferable". 24 Our optimized force field (Sundar/Sontum_old) reflects this philosophy. The final bond and angle parameters used are not taken from the NiOEP crystal structure. Instead these were assigned until the right geometric and vibrational fits was obtained. Table 4.3 lists the equilibrium values (req and [[theta]]eq in equation 2.1) used, the results of energy minimization using these parameters, and the corresponding results obtained from the crystal structure of NiOEP.
Table 4.3 Structural and Angle Parameters
Equilibrium Minimized NiOEP Crystal Structure
Values (Å or (Å or deg.) NiOEP (Å or
deg.) deg.) 19
19 BONDS
Ni-N 1.958 1.968 1.958
N-CC 1.376 1.381 1.376
CC-CB 1.443 1.453 1.443
CC-CD 1.371 1.377 1.371
CB-CB 1.346 1.350 1.346
CB-CX 1.495 1.516 1.510
CX-CY 1.501 1.512 1.506
CD-HM 1.090 1.086 1.090
CX(Y)-HE(N) 1.100 1.100 1.100
ANGLES
NP-NI-NP 180.000 179.822 180.000
NO-NI-NP 90.000 90.000 90.000
NI-N-CC 120.000 127.795 128.000
N-CC-CB 120.000 111.122 111.500
NO-CC-CD 121.800 125.018 124.000
CB-CC-CD 118.200 123.860 124.100
CC-N-CC 108.000 104.411 104.000
CC-CB-CB 120.000 106.673 106.500
CC-CD-CC 124.000 124.375 125.000
CC-CB-CX 120.000 127.537 125.500
CB-CB-CX 120.000 125.787 128.000
CB-CX-CY 109.500 110.103 109.500
BONDS
Ni-N 1.958 1.968 1.958
N-CC 1.376 1.381 1.376
CC-CB 1.443 1.453 1.443
CC-CD 1.371 1.377 1.371
CB-CB 1.346 1.350 1.346
CB-CX 1.495 1.516 1.510
CX-CY 1.501 1.512 1.506
CD-HM 1.090 1.086 1.090
CX(Y)-HE(N) 1.100 1.100 1.100
ANGLES
NP-NI-NP 180.000 179.822 180.000
NO-NI-NP 90.000 90.000 90.000
NI-N-CC 120.000 127.795 128.000
N-CC-CB 120.000 111.122 111.500
NO-CC-CD 121.800 125.018 124.000
CB-CC-CD 118.200 123.860 124.100
CC-N-CC 108.000 104.411 104.000
CC-CB-CB 120.000 106.673 106.500
CC-CD-CC 124.000 124.375 125.000
CC-CB-CX 120.000 127.537 125.500
CB-CB-CX 120.000 125.787 128.000
CB-CX-CY 109.500 110.103 109.500
A good force field upon minimization should reproduce the crystal structure
values for the various bond and angle, since a good geometry implies a good
energy fit for the molecule as well. As Table 4.3 shows, the Sundar/Sontum_old
force field reproduces both the bond lengths and bond angles seen in the X-ray
crystal structure of the NiOEP molecule. The average errors in the bond
lengths and angles listed in table 4.3 are 0.006 Å and 0.461deg.
respectively. Such accuracy is better than currently available in literature.
Other force fields, like Marques' MM2 force field reproduced porphyrin bond and
angle parameters with errors of 0.015 Å and 1.5deg. respectively.
22
Dihedral (Proper and Improper) Parameters
Unlike the IP parameters already described in this chapter, the OOP parameters developed in this thesis do not correspond to those developed by Dimmig. We broke away from using a single dihedral to describe all the proper dihedrals around a bond. Dimmig had also grouped his dihedrals into either cis or trans sets. We chose to define specific dihedrals for all the possible dihedrals. Table 4.4 shows the effects of this additional relaxation on the dihedral parameters used in the Sundar/Sontum_old force field. The proper dihedrals terms possible around the CB-CB bond are listed, and the values for these term in the Sundar/Sontum_old, Dimmig/Sontum and AMBER force fields are compared.
Table 4.4 Different Dihedral Parameters Definition Used.
Parameter AMBER Dimmig/ Sontum Sundar/
(kcal/mol) 18
18 (kcal/mol)
(kcal/mol) 24
24 Sontum_old
(kcal/ mol)
CC-CB-CB-CC 5.70 9.127 7.759
CX(Z)-CB-CB-CX(Z) 5.70 9.127 5.579
CC-CB-CB-CX(Z) 5.70 0.02 3.475
IMPROPER TERM 1.00 0.961 4.314
Total 21.80* 19.106* 20.645*
Sontum_old
(kcal/ mol)
CC-CB-CB-CC 5.70 9.127 7.759
CX(Z)-CB-CB-CX(Z) 5.70 9.127 5.579
CC-CB-CB-CX(Z) 5.70 0.02 3.475
IMPROPER TERM 1.00 0.961 4.314
Total 21.80* 19.106* 20.645*
* scaling formula used to account for improper term.As the last row of table 4.4 shows, consistency in the total rotation potential is maintained. The scaling procedure used to account for the improper terms is explained in Appendix C. Thus in the Sundar/Sontum_old force field, just as with smaller molecule force fields, the barrier to rotation has been distributed non-uniformly between such specific dihedrals term, and the additional flexibility has lead to better vibrational fits of the OOP modes. As a final check on the developed OOP force field, the intuitive consistency of the various parameters was evaluated. Just as bond force constants depend on the internuclear separation of atoms, i.e on the bond order, similarly we would also expect the total rotation potential around each bond to reflect the associated bond order. We summed up all the specific dihedrals around each bond and compared them to values listed in the AMBER force field. Table 4.5 lists the total potentials around each of the bonds and optimized values listed in the AMBER force field. The last column contains expected values based on bond orders. These values were used as a starting point for final values listed in the AMBER potential.
Table 4.5 Total Rotation Potentials.
Parameter Total Potential AMBER Expected
potential 25
25 Values
Values 18
18 X-NO-Ni-X (1.00) 7.122* 0.00 N.A.
X-CB-CX-X (1.00) 3.468* 1.10 0.00
X-CX-CY-X (1.00) 1.254 1.10* 0.00
X-CB-CB-X (1.75) 20.645* 21.80* 22.50
X-CB-CC-X (1.25) 11.101* 16.95* 7.50
X-CC-NO-X (1.50) 16.663* 15.95* 10.00
X-CC-CD-X (1.50) 10.259* 11.95* 14.50
X-NO-Ni-X (1.00) 7.122* 0.00 N.A.
X-CB-CX-X (1.00) 3.468* 1.10 0.00
X-CX-CY-X (1.00) 1.254 1.10* 0.00
X-CB-CB-X (1.75) 20.645* 21.80* 22.50
X-CB-CC-X (1.25) 11.101* 16.95* 7.50
X-CC-NO-X (1.50) 16.663* 15.95* 10.00
X-CC-CD-X (1.50) 10.259* 11.95* 14.50
*
improper terms accounted for using a scaling formula.units are kcal/mol
( ) refer to approximate bond orders
The total rotation potentials in almost all the cases agree with the values listed within the AMBER potential.Such consistency is reassuring as the total barrier to rotation around a bond should not depend on the distribution of the barrier. Most of the terms listed in the AMBER potential had improper terms, and the effects of these improper terms were accounted for by using a scaling formula (Appendix C). Thus, just as in the case of the benzene derivative (chapter III), the OOP parameters in Sundar/Sontum_old reflects a more dynamic and flexible force field.
Closer examination of Table 4.5, however, reveals 2 disagreement between dihedral parameters in the AMBER and Sundar/Sontum_old force fields. The AMBER force field has the proper dihedrals around both NO-Ni and CB-CX bonds set to zero. In our potential set, these parameters need definite values. These divergences are genuine, in that they reflect possible deficiencies in standard AMBER OOP parameter set itself, and need to be examined individually.
In the case of the dihedral defined around the Ni-N bond, the Sundar/Sontum_old force field diverges from the trend seen in the Karplus, Spiro and AMBER force fields. In all of these force fields, this dihedral has been set to zero. Vibrationally, the X-N-NI-X dihedrals control the frequency of the a low energy ruffling mode of the porphyrin. In our investigations of this mode, we found that a definite value for this Ni-N dihedral was required, to make this ruffling mode energetically demanding (i.e. have a non-zero vibrational frequency). The problem of zero frequency ruffling motion is particulary evident in the Karplus force field, which doesn't seem to have any other terms, which could restrict the ruffling motion. Our final X-N-Ni-X dihedral parameter was determined by matching the calculated ruffling mode frequency to the corresponding experimentally observed frequency.
The other parameter that does not correspond between the AMBER and Sundar/Sontum force fields is the total X-CB-CX-X torsion potential. AMBER has the proper dihedral around this bond set to zero. The only contribution to this term therefore is from an improper torsion term defined around the CB atom. Our analyses of ethylbenzene (Chapter 3) indicate, however, that there is non-zero proper dihedral rotation barrier around the CB-CX bond. We believe, therefore, that this term has been incorrectly set in the standard AMBER force field.
The last conclusion derived from our modeling of ethylbenzene was also transferred over to the porphyrin. With the additional flexibility in the proper dihedral set, we were able to eliminate the use of improper terms around most of the atom centers. Again, as we had observed in our analysis of ethylbenzene, we needed these improper terms only when hyperconjugation was possible. Therefore, use of improper terms was eliminated from the CD position of the porphyrin core. All other OOP modes could be satisfactorily reproduced using our specific, unrestricted proper dihedral parameter set.
Force Constants vs. Bond Lengths
After vibrational and structural consistency, another requirement of the final force field was that it display some intuitive consistency in the final parameters developed. Intuitively, one expects an inverse correlation to exist between bond lengths and associated force constants. Increasing the distance between atoms reduces their interaction with each other (reduces the bond order), hence one would expect the force constant to go down. While no linear relationship is expected, as the mass of the atoms at either ends of bond also needs to considered, a rough trend is expected. Relationships between the bond distances separating pairs of atoms and the force constant associated with these bond lengths were probed for the final force field. Figure 4.1 displays the trend seen in minimized structure, equilibrium bond lengths and force constants for the Sundar/ Sontum, Dimmig/ Sontum and Spiro force fields.
 Figure 4.1 Force Constant vs. Bond Length Trends
Figure 4.1 Force Constant vs. Bond Length Trends
The Spiro force field displays the expected intuitive trend between bond lengths and force constants. The Dimmig/ Sontum force field resembles the Spiro force field, even though force constants are consistently lower. Dimmig explained this in terms of the inverse relationship he had observed between averaged stretching and bending constants. As the Dimmig/ Sontum force field consistently has higher angle bending constants than the Spiro force field, lower bond force constants in the Dimmig/ Sontum force field were explained as another manifestation of this inverse trend. The only point which remained to be explained in the Dimmig/ Sontum force field was the CB-CZ bond length/ force constant relationship. The force constant was higher for this bond in the Dimmig/ Sontum force field than in the Spiro force field. The greater mass of the united ethyl atom (29 amu) as compared to the methyl atom used by Spiro was used to explain this discrepancy. It was hoped that when the united ethyl approximation was relaxed this inconsistent point would be corrected. 24
The inherent transferability of the Sundar/ Sontum and Dimmig/ Sontum force field is also evident from Figure 4.1. Almost all points in both these force fields coincide. As expected, lack of correspondence such correspondence is observed in parameters associated with the united ethyl approximation ( at bond length ~1.5 Å). The Sundar/Sontum_old force constant around ~1.5 Å are no longer greater than those listed in Spiro's force field. Such reordering supports Dimmig's hypothesis that the high united ethyl force constant (CB-CZ) was the result of the increased united ethyl mass.
Changing from a united ethyl model to our full NiOEP model, however, has not regained the relationship between force constants and bond lengths. Figure 4.1 shows a rise in the force constant around 1.5 Å for the Sundar/Sontum force field, even though bond lengths increase. All the bonds around ~1.5 Å are carbon-carbon bonds. The masses at either ends of the bonds are the same, and hence our intuitive feel for the force constant/ bond length relation should be satisfied. The resolution of this problem forms a basis for favoring the Sundar/Sontum_new force field (Chapter 5).
Our final force field reproduces the vibrational and structural features of NiP. Core porphyrin values from Sundar/ Sontum_old were transferred to NiP and parameters for the hydrogen atom were taken from the Dimmig optimized porphyrin force field. Table 4.3 lists [[chi]]2 values obtained when the Sundar/Sontum force field was applied to NiP. Minimized structural parameter values are also listed and compared to crystal structure values for this porphyrin.
Table 4.1 NiOEP force fields when applied to NiP
Minimized Values Crystal
Structure 21
21 [[chi]]2=2421.37
Bond
Ni-N 1.960 1.955
N-CC 1.381 1.380
CC-CB 1.443 1.440
CB-CB 1.343 1.352
CC-CD 1.379 1.383
ANGLES
CC-N-CC 104.063 104.8
N-CC-CB 111.176 110.7
CC-CB-CB 106.792 106.8
N-CC-CD 125.036 126.5
CC-CD-CC 123.992 121.4
[[chi]]2=2421.37
Bond
Ni-N 1.960 1.955
N-CC 1.381 1.380
CC-CB 1.443 1.440
CB-CB 1.343 1.352
CC-CD 1.379 1.383
ANGLES
CC-N-CC 104.063 104.8
N-CC-CB 111.176 110.7
CC-CB-CB 106.792 106.8
N-CC-CD 125.036 126.5
CC-CD-CC 123.992 121.4
The [[chi]]2 values of 2421 is comparable to the best fit obtained
by Jason Dimmig with his transferable force field ([[chi]]2
=2207.8). The average errors in bond lengths (0.005 Å) and angles
(1.45deg.) are again comparable with values obtained by others.
22
In conclusion, the Sundar/Sontum_old force field represents a transferable force field for the NiOEP porphyrin, developed by transferring parameters from ethylbenzene and the Dimmig/Sontum averaged force fields. Dihedral terms were reoptimized keeping in mind the conclusions arrived at in the previous chapter. The combined force field that resulted (Sundar/Sontum_old) produces better vibrational fits that other force fields present in the literature. Additionally, this force field is dynamic enough to reproduce the structural parameters of NiP as well. However, problems that still persist in this force field, have led to the development another force field (Sundar/Sontum_new). These problems will be reexamined in the following chapter (Chapter 5), where features of the new force field will be elaborated.
Chapter 5 New Approach to Modeling
The problems in our optimized force field (Sundar/ Sontum_old) mentioned in the previous chapter need to be summarized. A great range in force constants is evident in the angle bending constants (Table 4.2). This trend is evident in both the Sundar/ Sontum force field as well the Dimmig/ Sontum force field. While such a range did yield a better vibrational fit than the Spiro, Karplus or standard AMBER force fields, the simplicity characteristic of the AMBER force field is missing. Trends between bond lengths and force constants, which one would expect intuitively, also are not maintained across the range of bond lengths (Figure 4.1). While in the Dimmig/ Sontum force field such discrepancies were explained as the result of the increased CZ mass (Figure 4.1), such inconsistencies still persist in the Sundar/Sontum_old force field, where such mass arguments are no longer valid. As the Sundar/ Sontum force field is derived from the Dimmig/ Sontum force field, it is probable that there is a deficiency in that model as well. Finally, the Ni-N bond constant could not be selected without ambiguity. A range of values for this force constant is admissible within the Sundar/Sontum_old force field. To overcome the above mentioned problems another modeling philosophy was employed. The specifics of the modeling approach have been described in the methods section (Chapter 2). The results of using this modeling philosophy are evaluated in the following sections.
Vibrational
Fit
.
Any new force field has to reproduce the vibrations of NiOEP if it is to be
useful for the primary goal of this project. Table 5.1 compares the bond
stretch parameters in the Sundar/ Sontum (new) force field with values in the
present standard AMBER, Sundar/ Sontum (old), Spiro and Karplus force fields.
Table 5.1 Inplane Force Constant Comparison.
* Angle Force Constant units kcal mol-1
Only the core porphyrin parameters have been listed in Table 5.1. The
remaining ethyl group (bond and angle parameters) did not change much between
the old and new force fields. No significant changes were required in the OOP
parameters, hence these parameters have not been listed. The same restrictions
and approximations described in the previous chapter were employed while
listing the Karplus, AMBER and Spiro force fields. The [[chi]]2
values reflect the success of each of the force fields in reproducing the
experimentally observed frequencies when used in the AMBER software package.
The low [[chi]]2 value obtained with the Sundar/ Sontum_new force
field is indicative of the better vibrational fit obtained with this force
field.
Unlike the Sundar/ Sontum_old force field, some parameters of the Sundar/
Sontum_new force field find good matches in the Karplus force field, while the
AMBER provides better matches for the Ni-N force constant and the angle force
constants. The NiN force constant itself is more like force constants set in
the AMBER force field for heme porphyrins,
18
and should allow easier transfer of the NiOEP force field into the heme
porphyrin. The rough trend seen in the bond constants, seems to indicate that
these constants are indicative of the bond orders. Therefore, while the CB-CB
bond (bond order =1.75) has the highest force constant, the CC-CB bond (bond
order=1.25) has the lowest force constant.
Closer examination of the angle force constants and the Ni-N bond force
constants reveal the chief differences between the Sundar/ Sontum_new and
Sundar/ Sontum_old force fields. Each of these differences need to be examined
separately, in order to highlight the different modeling philosophies reflected
by the Sundar/Sontum_old and Sundar/Sontum_new force fields.
Sundar/Sontum_old vs. Sundar/Sontum_new Angle Force Constants
Sundar/ Sundar/ Spiro Karplus
*
Bond Force Constant units Kcal mol-1 Å-2 34
34 AMBER
AMBER 18
18 Sontum Sontum
Sontum Sontum  19-21
19-21 (new) (old)
[[chi]]2 1352 1656 5840.171 2684.301
BONDS
NI-NP 80.308 157.246 121.000 270.200 50.000
NP-CC 335.9 297.322 427.500 377.200 428.00
CC-CB 330.6 260.679 391.000 299.800 416.000
CC-CD 365.3 327.507 502.000 360.000 500.000
CB-CB 460.6 413.607 512.000 340.700 546.000
CD-HM 363.59 356.507 361.000 367.600 367.000
ANGLES
NP-NI-NP 0.000 0.000 0.000 0.000 0.000
NO-NI-NP 9.981 8.780 18.000 50.000 0.000
NI-NP-CC 80.289 87.705 22.000 96.150 0.000
NP-CC-CB 101.511 117.615 99.000 122.00 70.000
NP-CC-CD 43.77 36.191 60.000 88.000 70.000
CB-CC-CD 49.662 36.191 60.000 61.600 70.000
CC-NP-CC 62.010 130.413 117.00 139.300 70.000
CC-CB-CB 72.582 90.796 99.000 30.080 70.000
CC-CD-CC 92.601 166.070 79.000 94.200 70.000
CC-CD-HM 31.413 32.014 36.000 12.700 35.000
CC-CB-CX 26.414 29.230 86.000 65.000 70.000
CB-CB-CX 26.414 29.230 56.000 65.000 70.000
(new) (old)
[[chi]]2 1352 1656 5840.171 2684.301
BONDS
NI-NP 80.308 157.246 121.000 270.200 50.000
NP-CC 335.9 297.322 427.500 377.200 428.00
CC-CB 330.6 260.679 391.000 299.800 416.000
CC-CD 365.3 327.507 502.000 360.000 500.000
CB-CB 460.6 413.607 512.000 340.700 546.000
CD-HM 363.59 356.507 361.000 367.600 367.000
ANGLES
NP-NI-NP 0.000 0.000 0.000 0.000 0.000
NO-NI-NP 9.981 8.780 18.000 50.000 0.000
NI-NP-CC 80.289 87.705 22.000 96.150 0.000
NP-CC-CB 101.511 117.615 99.000 122.00 70.000
NP-CC-CD 43.77 36.191 60.000 88.000 70.000
CB-CC-CD 49.662 36.191 60.000 61.600 70.000
CC-NP-CC 62.010 130.413 117.00 139.300 70.000
CC-CB-CB 72.582 90.796 99.000 30.080 70.000
CC-CD-CC 92.601 166.070 79.000 94.200 70.000
CC-CD-HM 31.413 32.014 36.000 12.700 35.000
CC-CB-CX 26.414 29.230 86.000 65.000 70.000
CB-CB-CX 26.414 29.230 56.000 65.000 70.000
The angle force constants in the new force field do not display the same the fluctuation across the force field, as they did in the old force field. The fundamental effects of the changes made between the old and new force fields need to be examined to understand the reason for these for constants decreasing in the new force field.
The AMBER force field equation controlling the minimized bond lengths and angles contains the following two terms.
 Eq. 5.1
Eq. 5.1
Given a set of Kr, K[[theta]], req and [[theta]]eq values, the molecule is brought to its minimum energy structure by varying r and [[theta]] values before any vibrational analysis is done. Restoring forces, upon which the calculated frequencies depend, therefore depend on force constants (Kr or [[theta]]eq) and perturbation { (r-req)2 or ([[theta]]- [[theta]]eq)2} away from equilibrium. Previously, in the old force field approach, as indeed in Spiro's and Karplus' force fields, req and [[theta]]eq values were set to crystal structure values. A large force constant is required to produce the required restoring force. In the new force field, a different approach was taken. Unstrained req and [[theta]]eq values, determined by procedures described in the methods section, were used. This approach leads to fewer fluctuations in the angle force constants.
Nickel-Nitrogen Force Constant
The carboxyheme group we would like to examine has carbon monoxide bound to the metal center of the heme porphyrin. As a result any coupling of the porphyrin normal modes to the ligand vibrations will be transmitted through this metal center. Good assignment of this Ni-N force constant becomes critical, as the flexibility of the heme porphyrin core, and its effectiveness in transmitting potential coupling motions depend intimately on this choice. In the Sundar/Sontum_old force field this force constant could take on a range of values and still yield good vibrational and structural fits. The new modelling approach adopted in the Sundar/Sontum_new force field eliminates such ambiguity. We adjusted the value of the Ni-N force constant until a good structural fit for the Ni-N, minimized bond distance is obtained. Thereafter, other force constants were optimized to get good structural and vibrational fits. The additional, structural-fit criterion imposes restrictions on the choice of the Ni-N force constant, thereby eliminating the ambiguity that existed in the Sundar/Sontum_old force field. Lastly, the Ni-N force constant is closer to the Fe-N force constant used in the AMBER force field.
Bond length vs. Force Constants
A good vibrational fit was the first requirement of the optimized force field, and since the Sundar/ Sontum (new) force field satisfies this requirement, other stipulations, those of intuitive consistency and transferability, were applied to this force field.
The intuitive trend that one would expect between force constants and bond lengths was described in the previous chapter. The existence of such a trend in the new optimized force field would support adopting the Sundar/Sontum (new) force field over the Sundar/ Sontum (old) force field. Figure 5.1 is a graph, in which force constants have been plotted against minimized bond
lengths for the Sundar/ Sontum (new), Sundar/ Sontum (old) and Spiro force fields.
 Figure 5.1 Bond Length vs. Force Constants
Figure 5.1 Bond Length vs. Force Constants
As figure 5.1 shows, the intuitive trend that is expected between force constants and bond lengths is present in the new force field. Particularly around ~1.5 Å bond lengths, where such a trend was not maintained by the Sundar/ Sontum_old force field, this trend has been regained. The intuitive relationship between bond parameters and associated force constants is another reason for favoring the Sundar/ Sontum _new force field over the Sundar/Sontum_old force field.
A good geometric fit for NiOEP is also necessary, as inaccurate geometric fits are indicative of a poor energy fit for the molecule itself. Therefore, the ability of the Sundar/ Sontum (new) force field to reproduce crystal structure values of the porphyrin was examined. Table 5.2 lists the structural parameters input, the minimized molecules parameter values and the actual crystal structure values.
Table 5.2 Geometrical Fit.
Equilibrium Minimized NiOEP Crystal
Values (Å) (Å) Structure NiOEP
(Å)
BONDS
Ni-N 1.860 1.961 1.958
N-CC 1.380 1.381 1.376
CC-CB 1.440 1.450 1.443
CC-CD 1.380 1.378 1.371
CB-CB 1.350 1.356 1.346
CB-CX 1.501 1.515 1.510
CX-CY 1.506 1.512 1.506
CD-HM 1.090 1.086 1.090
CX(Y)-HE(N) 1.100 1.100 1.100
ANGLES
NP-NI-NP 180.00 179.818 180.000
NO-NI-NP 90.00 90.00 90.000
NI-N-CC 120.00 127.502 128.000
N-CC-CB 120.00 110.752 111.500
NO-CC-CD 120.00 126.421 124.000
CB-CC-CD 120.00 122.826 124.100
CC-N-CC 120.00 104.995 104.000
CC-CB-CB 120.00 106.750 106.500
CC-CD-CC 120.00 122.153 125.000
CC-CB-CX 120.00 125.982 125.500
CB-CB-CX 120.00 127.266 128.000
CB-CX-CY 109.5 110.240 109.500
It is evident from table 5.2 that the Sundar/ Sontum_new force field is capable
of reproducing the structural characteristics of the NiOEP molecule as well.
The minimized Ni-N bond length is only 0.003 Å larger than the crystal
structure values, again reinforcing our choice of 80.308 kcal/ Mol for this
force constant. The averaged error between the observed and calculated
structural parameters are small (0.006 Å for bond lengths and 1.201deg.
for angles). The relatively large error in the minimized angles seems to
result from the angles associated with the CD atom, particularly the CC-CD-CC
angle. However, the structural fit around this angle for the NiP (next section)
is good, indicating a possible deficiency in the our model itself. On average,
however, these errors are lower than those obtained in previous studies.
22
The last criterion applied on the Sundar/ Sontum (new) force field was one of transferability. As described in the previous chapter, the core porphyrin parameters were transferred to NiP. The vibrational and structural fits obtained upon transfer of this force field was examined. Table 5.3 lists the [[chi]]2 value, structural parameters obtained upon minimization, and crystal structure values for NiP.
Table 5.3 Structural and Vibrational Fits for NiP
Minimized Values Crystal Structure
[[chi]]2=2733
Bond
Ni-N 1.959 1.955
N-CC 1.377 1.380
CC-CB 1.443 1.440
CB-CB 1.353 1.352
CC-CD 1.375 1.383
ANGLES
CC-N-CC 105.571 104.8
N-CC-CB 110.279 110.7
CC-CB-CB 106.936 106.8
N-CC-CD 127.0 126.5
CC-CD-CC 121.408 121.4
The transferability of the Sundar/Sontum_new force field is evident in table
5.3. Average errors in the listed bond lengths and angles are 0.005 Å and
0.455deg. respectively. Again, such errors are below those obtained by others
in the literature.
22
Additionally, these errors are comparable with those obtained with the Sundar/
Sontum_old force field (0.005 Å and 1.45deg.). Lastly, the
[[chi]]2 value with this force field is higher than that calculated
with the Dimmig/Sontum force field. This higher [[chi]]2 value
reflects the emphasis of this thesis- a good vibrational fit for NiOEP, and the
linear weighting scheme (all weights set to 1) used while calculating the
[[chi]]2 values for NiP. Therefore, even though key frequencies find
better matches with the Sundar/Sontum_new force field, such better
correspondence is not reflected in the [[chi]]2 value.The Sundar/Sontum_new force field satisfies all the requirements of the new force field. It is transferable between NiOEP and NiP, accurately reproducing structural and vibrational features for both of these molecules. Large fluctuations in angle force constants are avoided, and intuitive trends are observed in the bond constants. All of these factors strongly recommend usage of the new modeling approach described in the methods section. This transferable Sundar/Sontum_new force field was transferred over to the heme porphyrin, once appropriate force constants for the Fe-N bond had been determined.
Chapter 6 Heme Porphyrin Analysis
As the Sundar/Sontum_new force field for NiOEP proved to be a consistent, transferable force field, a heme force field could be developed from it. Obviously, force field parameters had to be determined for parameters associated with the iron-metal center and additional functional groups at the periphery of protoporphyrin IX. Fortunately, the inherent modeling philosophy of the Sundar/Sontum_new force field made the choice of the Fe-N force constants relatively straightforward, and standard force field parameters could be used for the additional peripheral groups. As indicated previously, the choice of the metal-nitrogen force constant is critical, as the flexibility of the porphyrin core and its ability to couple vibrationally with attached ligands depend intimately on an appropriate choice of this constant. We set the value of the Fe-N force constant to 71.0 kcal/ Mol in the heme porphyrin, quite similar to the Ni-N force constant selected in the Sundar/Sontum_new force field. Our justifications for this force constant choice will be elaborated in the next section.
The ambiguity in nickel-nitrogen force constant, present with the Sundar/Sontum_old force field, was satisfactorily resolved with the Sundar/Sontum_new force field, especially as our choice of this constant was controlled by both structural and vibrational requirements imposed on the force field. The inherent transferability of our new force field and available structural data on iron porphyrin system were exploited to yield experimentally consistent values for iron related parameters. The Fe-N force constant was varied until the iron-nitrogen distance in iron octaethyl porphyrin (FeOEP) agreed with average structural values calculated for iron porphyrin systems. The final values chosen for the Fe-N constant was 71.0 Kcal/mol, while the unstrained equilibrium distance was set to 1.93 Å. The reason for the choosing an equilibrium distance of 1.93 Å was described in the methods section. Table 6.1 lists the structural parameters calculated for iron octaethyl porphyrin, when the above mentioned parameter values were chosen, and average observed values for intermediate spin, four coordinate iron (II) complexes. 22
Table 6.1 Structural Parameters for Iron Octaethyl Porphyrin (FeOEP)
Parameter Calculated (Å) Observed (Å)As table 6.1 demonstrates, our FeOEP structural parameters match average observed values, thus our choice of Fe-N force constant value of 110.308 kcal/ mol is experimentally consistent. We chose to fit our FeOEP values to averaged, four coordinate iron porphyrin values, so that the Fe-N parameter would be more easily transferred to the heme porphyrin.22
Fe-Np 1.979 Å 1.979 (0.015) Np-Fe-Np (trans) 180.00 deg. 179.1deg. (0.9) Np-Fe-Np (cis) 90.0deg. 90.0deg. (0.3)
Once the consistency of the iron related parameters was ensured, as a further check we compared the remaining porphyrin parameters with their mean values in Fe(II)and Fe(III) porphyrins. The results of such comparison are shown in Table 6.2, in which non-iron related structural parameters are compared with their averaged values.
Table 6.2 Non-Iron Structural Parameters in FeOEP
Parameter Calculated Average Observed22
BOND N-CC 1.379 1.380 (0.013) CC-CD 1.382 1.389 (0.016) CC-CB 1.450 1.439 (0.018) CB-CB 1.358 1.350 (0.022) ANGLE CC-N-CC 105.584 105.8 (1.1) N-CC-CB 110.375 109.9 (1.1) CC-CB-CB 106.833 107.2 (1.0) CC-CD-CC 122.606 124.6 (1.8) N-CC-CD 126.489 125.4 (1.3) CB-CC-CD 123.135 124.6 (1.8)
As Table 6.2 shows, structurally the FeOEP parameters agree with averaged experimental values for iron porphyrins. Standard errors between the calculated and averaged values are 0.008 Å and 1.33 deg. respectively for bonds and angles. Such agreement reinforces the structural consistency of the Sundar/Sontum_new force field and the Fe-N constants, that were chosen.
The other major group that still remained to be modeled was the vinyl group at the periphery of the porphyrin molecule. Specifically, the rotational potential of the vinyl group was modeled by examining styrene. Our interest in the rotational potential of the vinyl group was raised, primarily because of the trend observed in our examinations of ethylbenzene. To summarize, the standard AMBER force field has the rotational potentials around a CC-CX bond set to zero. As discussed in chapter 3, this value is unrealistically low, because semi-empirical calculations done with Spartan indicate otherwise. Therefore, the default rotational potential around the vinyl-porphyrin bond, which is set to zero in AMBER, was recalculated. In a manner similar to the method used in ethylbenzene (chapter 3), we calculated the torsional barrier around the vinyl-benzene bond in styrene using Spartan. Fourier analysis of this potential revealed the existence of predominant two-fold term, which was then transferred over to styrene's force field and optimized. The total torsion barrier (Vn in equation 2.1) optimized on styrene was 1.624 kcal/mol. Lack of vibrational data on for heme porphyrins precluded further optimization on the porphyrin. But, as the two-fold rotational potential from ethylbenzene had proved itself to be transferable to NiOEP (chapter 3), we felt confident transferring the two fold rotational potential parameters over from styrene to heme. A more complete analysis of styrene, however remains to be done.
Our final heme force field was used to address the original questions posed by the different frequency assignments made by the Spiro and Kitagawa groups. With a consistent force field, we computationally recreated the isotopic shift experiments performed by the Spiro and Kitagawa groups, and addressed the Spiro/Kitagawa controversy from another perspective. First, we varied Fe-C and C-O force constants, until our calculated [[upsilon]](Fe-CO) and [[upsilon]](C-O) frequencies matched experimentally observed ones. Then we set the Fe-C-O bending force constant, until either the Spiro or Kitagawa assigned bending frequency was matched. Thereafter, we varied the mass of both the carbon and oxygen atoms in the carbon monoxide ligand, and analyzed, using the NMANAL module, the effects of such mass changes on the vibrational frequencies. Our hope was to simulate the isotopic shift patterns seen by either one of the groups for the d(FeCO) frequency. Table 6.2 summarizes the results of such isotopic shift simulations, after either Spiro or Kitagawa assignment of d(FeCO) frequency had been matched.
Along with the Spiro and Kitagawa assignments and isotopic shift data, 10,12 calculated values for these frequencies have also been listed in Table 6.4. The absolute shift in frequency upon isotopic substitution is listed for individual group experiments and our simulations. Unlike the observed frequencies, we noticed multiple bands in the same frequency, which were sensitive to changes into the CO ligand mass. To make our comparison and analysis of subsequent data easier, only bands which had at least a 10% PED on one of the FeCO parameters, are listed in table 6.4. The PED values for the various bands were obtained from the NMANAL module's output . The [[upsilon]](CO) and [[upsilon]](FeC) frequencies assignments are not disputed in the literature, as both groups have assigned comparable values to these bands. These bands, however, are included in table 6.4 to gauge the accuracy the heme force field.
It is immediately evident, that the force field accurately reproduces the observed [[upsilon]](CO) frequencies and shift patterns. Such accuracy, however, eludes force field calculations when the [[upsilon]](FeC) frequencies are examined. While the absolute frequency is reproduced accurately, when either the Spiro or Kitagawa frequencies assignment is simulated, the isotopic shift pattern is not reproduced in either cases. The magnitude of isotopic shifts is calculated to be much smaller in our force field than is actually observed. Further analysis of the bands around 500 cm-1 revealed one possible explanation for this discrepancy. The PED of the [[upsilon]](FeC) frequency in both sets of simulations is not 100% FeC stretch, i.e. the character is not entirely a FeC bond stretch. Though too small, the monotonically decreasing pattern observed by the Kitagawa and Spiro groups for this frequency is simulated- [[upsilon]](FeC) decreases as the mass of the CO unit is raised.
The results of our d(FeCO) simulations are more clear cut. By varying the Fe-C-O angle force constant, we reproduce the characteristic "zig-zag" pattern of frequency shifting for either the Spiro or Kitagawa group. Our Kitagawa group assignment simulations are deficient, however, in that we are not able to simulate the right magnitude of isotopic shift patterns for the d(FeCO) frequency. Furthermore, multiple bands are calculated to be sensitive to such isotopic substitution. By reducing the d(FeCO) force constant to reproduce the approximate magnitude for the Kitagawa group assignments, more mixing of the bending mode is observed. Physically, such increased mixing is evident from the multiple, isotopic-substitution sensitive bands. Additionally, the magnitude of the d(FeCO) shift upon increasing the mass of the carbon atom in CO is much smaller in our simulations than observed by the Kitagawa group. Analyzing the PED of this vibrational mode provides an explanation. The PED of this bending frequency is not 100% d(FeCO), instead the d(FeCO) bending character is dispersed over multiple frequencies. In the case of the Spiro simulations, only three d(FeCO) frequencies are seen. Not much coupling of the bending mode takes place; the character of the FeCO bending mode is close to 60% for one of the bands. As a result this bending frequency bands displays the same magnitude in its shift pattern. Therefore, the Spiro group's assignments seem to be favored by our model.
Myoglobin
Protein Effects
As indicated in the methods section, analysis of carboxyheme vibrations was not
done within the protein itself. A glitch in the AMBER NMODE module prevented
such simulations. Instead, we used results calculated by Maggie Zraly to
predict possible geometrical repercussions of modeling the Kitagawa and Spiro
group assignments.
In order to reproduce either the Kitagawa or Spiro group assignments for the d(FeCO) motion, we varied the Fe-C-O bend constant. Table 6.5 lists the final sets of parameter values required to simulate the Kitagawa and Spiro group assignments.
Table 6.5 Final Force Constants
K(Fe-C) K(C-O) K(Fe-C-O)
Spiro 160 1044 68.00
Kitagawa 160 1044 22.00
*
Bond Force constant units Kcal mol-1 Å-2 * Angle Force constant units Kcal mol-1
As Table 6.5 indicates, the only force constant that was changed between our simulations of the Kitagawa and Spiro group results was the Fe-C-O angle force constants. The value of this force constant is 68. kcal mol-1 in the case of the Spiro simulations, while a force constant of 22 kcal mol-1 was required to reproduce the Kitagawa group assignments.
Different researchers have considered with the effect of the protein on the CO ligand's orientation within the protein. Recent crystal structures indicate that this linkage is linear. 9 Maggie Zraly determined a relationship between the Fe-C-O force constant and the angle of the FeCO linkage would adopt within the myoglobin protein. She computed the effects of the protein framework upon minimization on the FeCO linkage for a given set of force constants. Figure 6.1 shows the results that she had derived.
Figure 6.1 Fe-C-O Angle vs. Force Constant 23
If figure 6.1 is used to predict the final geometry of the FeCO linkage within the protein environment, then the unreasonableness of the Kitagawa group's assignments is apparent. The force constant of 28.00 kcal mol-1 would cause the FeCO linkage to adopt a bent structure (FeCO angle of 175deg.). The Spiro assignment force constant, however, would allow the FeCO linkage to retain a linear geometry within the protein. Thus the Spiro assignment would allow the FeCO geometry predicted by our force field to be consistent with crystal structure. 9 Therefore, even within the protein we would expect our model to geometrically favor the Spiro assignment of the d(FeCO) frequency.
Chapter 7- Conclusions and Future Work
The focus of this thesis was to analyze the vibrations of carboxyheme using a consistent, transferable force field. Our interest in this porphyrin system arouse because of the controversy surrounding the exact bending frequency for the Fe-CO linkage in the carboxy porphyrin. We have successfully developed a force field for the heme porphyrin, by transferring over a consistent force field from nickel porphyrin system, and analyzed the carboxyheme system. Our analysis outside the protein supports the Spiro group's assignments for this frequency. We were unable to perform these calculations within the protein environment, and directly prove the Spiro group assignments. However, calculations done using results obtained by Zraly reinforce the unreasonableness of the Kitagawa group's assignments.
In our attempts to develop a consistent force field for nickel octaethyl porphyrin, we examined other smaller molecules. Conclusions from such analyses were then used in our modeling of NiOEP. The main conclusion that were transferred are the following. More specific definitions for dihedral terms help in improving vibrational fits for the OOP modes of vibrations. The overall barrier to rotation usually remains constant but the internal distribution of this barrier is non-uniform. The resulting increase in the force field's flexibility helps to improve vibrational fits and exclude improper terms. In fact, improper torsion terms are needed only when hyperconjugation effects need to simulated.
Lastly, we were able to develop two consistent force field for NiOEP. The first force field was developed from the force field developed by Jason Dimmig. The similarity between the two force field (Dimmig/Sontum and Sundar/Sontum_old) emphasizes the inherent transferability of these force fields. A second force field, reflecting a different modeling philosophy, was also developed. A fundamental change in modeling was effected in the second force field. Equilibrium distances angles were set using unstrained literature values, and force constants were then varied to get good vibrational and structural fits. Greater uniformity and intuitive consistency is evident in the parameter set, when such a change in modeling is effected.
As indicated in the conclusion, no simulations were possible within the protein environment, and therefore a fundamental goal of this project stills remains to be done. The AMBER force field package has some glitches in it, which do not allow the use of the IBELLY option for vibrational analysis. Once these "bugs" have been corrected, analysis within the protein can be concluded. The effects of the protein environment on this linkage can then be fully explored.
With the existence of a good parameter set for the heme group, it should be possible to examine other questions concerning the myoglobin and hemoglobin proteins. Specifically, the spectroscopically different vibrational states 8 of carboxyheme group can be probed computationally. Pathways for ligand escape upon photodissociation may also be examined. 34
Finally, parameter set for other important molecules may be undertaken, using some of the modeling conclusions determined in this project. Thus, modeling of nucleic acids can be done and inherent deficiencies in standard parameter describing these molecules may be eliminated, in a manner similar to the corrections done for the heme porphyrin set.
 (1)
Lehninger, A., L In Biochemistry; second ed.Worth: New York, 1975; pp
137-138.
(1)
Lehninger, A., L In Biochemistry; second ed.Worth: New York, 1975; pp
137-138.
(2) Spiro, T. G.; Vogel, K. M.; Hu, S. Journal of the American Chemical Society 1994, 116, 11187-11188.
(3) Alberty, R., A; Silbey, R., J In Physical ChemistryJohn Wiley and Sons: New York, 1992; pp 489-491.
(4) Collman, J. P.; Brauman, J. I.; Halbert, T. R.; Suslick, K. S. Proceedings of the National Academy of Science 1976, 73, 3333-3337.
(5) Spiro, T. G.; Li, X. Y.; Ibers, J. A.; Sessler, J. L.; Ray, G. B. Journal of the American Chemical Society 1994, 116, 162-176.
(6) Peng, S., M; Ibers, J., A Journal of the American Chemical Society 1976, 98, 8032.
(7) Kuriyan, J.; Wilz, S.; Karplus, M.; Petsko, G., O Journal of Molecular Biology 1992, 196, 133-154.
(8) Lim, L.; Jackson, T., A Journal of Chemical Physics 1995, 102, 4355--4366.
(9) Quillin, M., L; Arduini, R., M; Olson, J., S; Phillips Journal of Molecular Biology 1993, 234, 140-155.
(10) Spiro, T. G.; Y, L. X. Journal of the American Chemical Society 1988, 111, 6024--6033.
(11) Kitagawa, T.; Takashi, O.; Hirota, S. Journal of the American Chemical Society 1995, 117, 821-822.
(12) Kitagawa, T.; Hirota, S.; Ogura, T. Journal of Physical Chemistry 1994, 98, 6652--6660.
(13) Tsubaki, M.; Srivastava, R. B.; Yu, N. T. Biochemistry 1982, 21, 1132-1140.
(14) Kitagawa, T.; Yamamoto, S.; Minoato, T.; Saito, M.; Jewsbury, P. Journal of the American Chemical Society 1994, 116, 11586-11587.
(15) Allinger, N., L.; Burkert, U. In Molecular MechanicsAmerican Chemical Society: New York, 1982; Vol. 177; pp 14-56.
(16) Allinger, N., L; Burkert, U. In Molecular Mechanics; First ed.American Chemical Society: Washington D.C., 1982; Vol. 177; pp ix-xii.
(17) Decius, J.; Cross, P. C.; Wilson, E. B. J. The Theory of Infrared and Raman Vibrational Spectra; McGraw-Hill Book Company: New York, 1955.
(18) Kollman, P. A.; Cornell, W. D.; Cieplak, P.; Bayly, C. I. Journal of the American Chemical Society 1995, 117, 5179-5197.
(19) Li, X. Y.; Czernuszewicz, R. S.; Kincaid, J. R.; Su, Y. O.; Spiro, T. G. Journal of Physical Chemistry 1990, 94, 31-47.
(20) Li, X. Y.; Czernuszewicz, R. S.; Kincaid, J. R.; Stein, P.; Spiro, T. G. Journal of Physical Chemistry 1990, 94, 47-61.
(21) Li, X. Y.; Zgierski, M. Z. Journal of Physical Chemistry 1991, 95, 4268-4287.
(22) Marques, H. M.; Munro, O. Q.; Markoulides, T. Journal of Chemical Society Faraday Transactions 1995, 91, 1741-1749.
(23) Zraly, M. A. Senior-honors Thesis, Middlebury College, 1995.
(24) Dimmig, J. Senior Thesis, Middlebury College, 1995.
(25) Pearlman, D. A.; Case, D. A.; Caldwell, J. W.; Kollman, P. A. In University of California: San Franscisco, 1994; pp .
(26) Scheidt, W. R.; Reed, C. R. Chemical Review 1981, 81, 543--555.
(27) Hoard, J. L. ; 199?
(28) Bevington, P. R. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill Book Company: New York, 1969.
(29) Mead, R.; Nelder, J. A. Computer Journal 1965, 7, 308-311.
(30) Kincaid, J. R.; Urban, M. W.; Watanabe, T.; Nakamoto, K. Journal of Physical Chemistry 1983, 87, 3096-3101.
(31) Lau, C. L.; Snyder, R. G. Spectrochimica Acta. 1970, 27A, 2073--2088.
(32) Lau, C. L.; Snyder, R. G. Spectrochimica Acta 1973, ???, ???
(33) Jorgensen, W. L.; Maxwell, D. S.; Tirado-Rives, J. Journal of Computational Chemistry 1995, 16, 984--1010.
(34) Karplus, M.; Kuriyan, J.; Kuczera, K. Journal Molecular Biology
1990, 213, 351--373.

0 0 2
benzene prep file
benzene.db3
BEN INT 1
CORR NOMIT DU BEG
0.00000
1 DUMM DU M 0 -1 -2 0.0000 0.0000 0.0000 0.0000
2 DUMM DU M 1 0 -1 1.0000 0.0000 0.0000 0.0000
3 DUMM DU M 2 1 0 1.0000 90.0000 0.0000 0.0000
4 C1 CA M 3 2 1 1.4000 90.0000 90.0000 -0.1500
5 H1 HA E 4 3 2 1.0900 90.0000 0.0000 0.1500
6 C2 CA B 4 3 2 1.4000 90.0000 120.0000 -0.1500
7 H2 HA E 6 4 3 1.0900 120.0000 -90.0000 0.1500
8 C3 CA B 6 4 3 1.4000 120.0000 90.0000 -0.1500
9 H3 HA E 8 6 4 1.0900 120.0000 180.0000 0.1500
10 C4 CA B 8 6 4 1.4000 120.0000 0.0000 -0.1500
11 H4 HA E 10 8 6 1.0900 120.0000 180.0000 0.1500
12 C5 CA B 10 8 6 1.4000 120.0000 0.0000 -0.1500
13 H5 HA E 12 10 8 1.0900 120.0000 180.0000 0.1500
14 C6 CA S 12 10 8 1.4000 120.0000 0.0000 -0.1500
15 H6 HA E 14 12 10 1.0900 120.0000 180.0000 0.1500
LOOP
C1 C6
IMPROPER
C6 C2 C1 H5
C1 C3 C2 H2
C4 C2 C3 H3
C5 C3 C4 H4
C6 C4 C5 H1
C5 C1 C6 H6
DONE
STOP
0 0 2
ethybenzene prep file
toluene.db3
TOL INT 1
CORR NOMIT DU BEG
0.00000
1 DUMM DU M 0 -1 -2 0.0000 0.0000 0.0000 0.0000
2 DUMM DU M 1 0 -1 1.0000 0.0000 0.0000 0.0000
3 DUMM DU M 2 1 0 1.0000 90.0000 0.0000 0.0000
4 C1 CA M 3 2 1 1.5100 90.0000 90.0000 -0.1101
5 H1 HA E 4 3 2 1.0900 90.0000 0.0000 0.1399
6 C2 CA B 4 3 2 1.4000 90.0000 120.0000 -0.1601
7 H2 HA E 6 4 3 1.0900 120.0000 -90.0000 0.1399
8 C3 CA B 6 4 3 1.4000 120.0000 90.0000 -0.1601
9 H3 HA E 8 6 4 1.0900 120.0000 180.0000 0.1399
10 C4 CA B 8 6 4 1.4000 120.0000 0.0000 -0.1601
11 H4 HA E 10 8 6 1.0900 120.0000 180.0000 0.1399
12 C5 CA B 10 8 6 1.4000 120.0000 0.0000 -0.1601
13 H5 HA E 12 10 8 1.0900 120.0000 180.0000 0.1399
14 C6 CA S 12 10 8 1.4000 120.0000 0.0000 -0.1601
15 C7 CT 3 14 12 10 1.5100 120.0000 180.0000 -0.1184
16 C8 CT 3 14 12 10 1.5260 109.5000 90.0000 -0.1184
17 H81 HM E 16 15 14 1.0900 109.5000 0.0000 0.0896
18 H82 HM E 16 15 14 1.0900 109.5000 120.0000 0.0896
19 H83 HM E 16 15 14 1.0900 109.5000 -120.0000 0.0896
20 H72 HC E 15 14 12 1.0900 109.5000 -30.0000 0.0896
21 H73 HC E 15 14 12 1.0900 109.5000 -150.0000 0.0896
LOOP
C1 C6
IMPROPER
C1 C2 H2 C3
C2 C3 H3 C4
C3 C4 H4 C5
C4 C5 H5 C6
C5 C6 C7 C1
C6 C1 H1 C2
H1 C6 C1 C2
H2 C1 C2 C3
H3 C2 C3 C4
H4 C3 C4 C5
H5 C4 C5 C6
C7 C5 C6 C1
DONE
STOP
0 0 2
Heme-histidine residue ALL ATOM, Yves names .1 CO charge nuetron coord
heme_his_co.db3
HEM INT 1
CORRECT NOMIT DU BEG
0.00000
1 DUMM DU M 0 -1 -2 0.0000 0.0000 0.0000 0.0000
2 DUMM DU M 1 0 -1 1.4490 0.0000 0.0000 0.0000
3 DUMM DU M 2 1 0 1.5220 111.1000 0.0000 0.0000
4 N N M 3 2 1 1.3350 116.6000 180.0000 -0.4630
5 HN H E 4 3 2 1.0100 119.8000 0.0000 0.2520
6 CA CT M 4 3 2 1.4490 121.9000 180.0000 0.0350
7 HA HC E 6 4 3 1.0900 109.5000 300.0000 0.0480
8 CB CT 3 6 4 3 1.5250 111.1000 60.0000 -0.0980
9 HB2 HC E 8 6 4 1.0900 109.5000 60.0000 0.0380
10 HB3 HC E 8 6 4 1.0900 109.5000 300.0000 0.0380
11 CG CC S 8 6 4 1.5100 115.0000 180.0000 -0.0320
12 ND1 NA B 11 8 6 1.3900 122.0000 180.0000 -0.1460
13 HND H E 12 11 8 1.0100 126.0000 0.0000 0.2280
14 CE1 CR B 12 11 8 1.3200 108.0000 180.0000 0.2410
15 HE HC E 14 12 11 1.0800 120.0000 180.0000 0.0360
16 NE2 NB B 14 12 11 1.1300 109.0000 0.0000 -0.5020
17 CD2 CV S 16 14 12 1.3600 110.0000 0.0000 0.1950
18 HD HC E 17 16 14 1.0800 120.0000 180.0000 0.0180
19 FE FE B 16 14 12 2.1000 124.0000 180.0000 0.2500
20 NA NP S 19 16 14 2.0800 98.0000 90.0000 -0.1800
21 C1A CC S 20 19 16 1.3800 125.4000 90.0000 0.0300
22 C2A CB B 21 20 19 1.4100 109.0000 180.0000 -0.0200
23 CAA CX 3 22 21 20 1.5100 124.0000 180.0000 -0.1600
24 HP71 HE E 23 22 21 1.0900 109.5000 60.0000 0.1000
25 HP72 HE E 23 22 21 1.0900 109.5000 300.0000 0.1000
26 CBA CY 3 23 22 21 1.5400 111.0000 180.0000 -0.3000
27 HP73 HN E 26 23 22 1.0900 109.5000 60.0000 0.1000
28 HP74 HN E 26 23 22 1.0900 109.5000 300.0000 0.1000
29 CGA C B 26 23 22 1.5270 109.4000 180.0000 0.3000
30 O1A O2 E 29 26 23 1.2600 117.2000 90.0000 -0.5000
31 O2A O2 E 29 26 23 1.2600 117.2000 270.0000 -0.5000
32 C3A CB B 22 21 20 1.4100 107.0000 0.0000 0.0200
33 CMA CX 3 32 22 21 1.5100 125.0000 180.0000 -0.2650
34 HM81 HE E 33 32 22 1.0900 109.5000 60.0000 0.0750
35 HM82 HE E 33 32 22 1.0900 109.5000 180.0000 0.0750
36 HM83 HE E 33 32 22 1.0900 109.5000 300.0000 0.0750
37 C4A CC S 32 22 21 1.4100 107.0000 0.0000 0.0200
38 CHB CD B 37 32 22 1.3700 127.0000 180.0000 -0.1100
39 HDM HM E 38 37 32 1.0800 120.0000 0.0000 0.1500
40 C1B CC B 38 37 32 1.3700 127.0000 180.0000 0.0300
41 NB NO E 40 38 37 1.3800 124.0000 0.0000 -0.1800
42 C2B CB B 40 38 37 1.4100 127.0000 180.0000 0.0200
43 CMB CX 3 42 40 38 1.5100 125.0000 0.0000 -0.2650
44 HM11 HE E 43 42 40 1.0900 109.5000 60.0000 0.0750
45 HM12 HE E 43 42 40 1.0900 109.5000 180.0000 0.0750
46 HM13 HE E 43 42 40 1.0900 109.5000 300.0000 0.0750
47 C3B CB B 42 40 38 1.4100 107.0000 180.0000 -0.0500
48 CAB CQ B 47 42 40 1.5100 126.0000 180.0000 -0.1300
49 HV2A HQ E 48 47 42 1.0800 120.0000 0.0000 0.1500
50 CBB CQ B 48 47 42 1.3300 120.0000 180.0000 -0.3000
51 HV2C HQ E 50 48 47 1.0800 120.0000 0.0000 0.1000
52 HV2T HQ E 50 48 47 1.0800 120.0000 180.0000 0.1000
53 C4B CC S 47 42 40 1.4100 107.0000 0.0000 0.0200
54 CHC CD B 53 47 42 1.3700 127.0000 180.0000 -0.1100
55 HAM HM E 54 53 47 1.0800 120.0000 0.0000 0.1500
56 C1C CC B 54 53 47 1.3700 130.0000 180.0000 0.0300
57 NC NP E 56 54 53 1.3800 124.0000 0.0000 -0.1800
58 C2C CB B 56 54 53 1.4100 127.0000 180.0000 0.0200
59 CMC CX 3 58 56 54 1.5100 125.0000 0.0000 -0.2650
60 HM31 HE E 59 58 56 1.0900 109.5000 60.0000 0.0750
61 HM32 HE E 59 58 56 1.0900 109.5000 180.0000 0.0750
62 HM33 HE E 59 58 56 1.0900 109.5000 300.0000 0.0750
63 C3C CB B 58 56 54 1.4100 107.0000 180.0000 -0.0500
64 CAC CQ B 63 58 56 1.5100 126.0000 180.0000 -0.1200
65 HV4A HQ E 64 63 58 1.0800 120.0000 0.0000 0.1500
66 CBC CQ B 64 63 58 1.3300 120.0000 180.0000 -0.3000
67 HV4C HQ E 66 64 63 1.0800 120.0000 0.0000 0.1000
68 HV4T HQ E 66 64 63 1.0800 120.0000 180.0000 0.1000
69 C4C CC S 63 58 56 1.4100 107.0000 0.0000 0.0200
70 CHD CD B 69 63 58 1.3700 127.0000 180.0000 -0.1100
71 HBM HM E 70 69 63 1.0800 120.0000 0.0000 0.1500
72 C1D CC B 70 69 63 1.3700 130.0000 180.0000 0.0300
73 ND NO E 72 70 69 1.3800 124.0000 0.0000 -0.1800
74 C2D CB B 72 70 69 1.4100 127.0000 180.0000 0.0200
75 CMD CX 3 74 72 70 1.5100 125.0000 0.0000 -0.2650
76 HM51 HE E 75 74 72 1.0900 109.5000 60.0000 0.0750
77 HM52 HE E 75 74 72 1.0900 109.5000 180.0000 0.0750
78 HM53 HE E 75 74 72 1.0900 109.5000 300.0000 0.0750
79 C3D CB B 74 72 70 1.4100 107.0000 180.0000 -0.0200
80 C4D CC S 79 74 72 1.4100 107.0000 0.0000 0.0200
81 CHA CD S 80 79 74 1.3700 127.0000 180.0000 -0.1100
82 HGM HM E 81 80 79 1.0800 120.0000 0.0000 0.1500
83 CAD CX 3 79 74 72 1.5100 124.0000 180.0000 -0.1600
84 HP61 HE E 83 79 74 1.0900 109.5000 60.0000 0.1000
85 HP62 HE E 83 79 74 1.0900 109.5000 300.0000 0.1000
86 CBD CY 3 83 79 74 1.5400 111.0000 180.0000 -0.3000
87 HP63 HN E 86 83 79 1.0900 109.5000 60.0000 0.1000
88 HP64 HN E 86 83 79 1.0900 109.5000 300.0000 0.1000
89 CGD C B 86 83 79 1.5300 109.4000 180.0000 0.3000
90 O1D O2 E 89 86 83 1.2600 117.2000 90.0000 -0.5000
91 O2D O2 E 89 86 83 1.2600 117.2000 270.0000 -0.5000
92 CMX LC S 19 16 14 2.1100 180.0000 90.0000 0.1000
93 OMX LO E 92 19 16 1.2000 170.0000 0.0000 -0.1000
94 C C M 6 4 3 1.5220 111.1000 180.0000 0.6160
95 O O E 94 6 4 1.2290 120.5000 0.0000 -0.5040
LOOP EXPLICIT
NA C4A
FE NB
FE NC
FE ND
NB C4B
NC C4C
ND C4D
C1A CHA
CG CD2
IMPROPER
C1A CHA HGM C4D
C1D CHD HBM C4C
C1C CHC HAM C4B
C1B CHB HDM C4A
C1A NA FE C4A
C1B NB FE C4B
C1C NC FE C4C
C1D ND FE C4D
C1A C2A CAA C3A
C1B C2B CMB C3B
C1C C2C CMC C3C
C1D C2D CMD C3D
C2A C3A CMA C4A
C2B C3B CAB C4B
C2C C3C CAC C4C
C2D C3D CAD C4D
C1B NB CHB C2B
C1A NA CHA C2A
C1D ND CHD C2D
C1C NC CHC C2C
DONE
STOP
Nickel octaethyl porphine Prep File
0 0 2
Nioep with non-united methyl groups CY 7-14-95 leanear dihedral warning
por_beg.db3
POR INT 1
CORRECT NOMIT DU BEG
0.00000
1 DUMM DU M 0 -1 -2 0.0000 0.0000 0.0000 0.0000
2 DUMM DU M 1 0 -1 1.0000 0.0000 0.0000 0.0000
3 DUMM DU M 2 1 0 1.0000 90.0000 0.0000 0.0000
4 NI NI M 3 2 1 2.1100 90.0000 90.0000 0.2219
5 NA NP S 4 3 2 1.9580 90.0000 90.0000 -0.2081
6 C1A CC S 5 4 3 1.3760 128.0000 -90.0000 0.0019
7 C2A CB B 6 5 4 1.4430 111.5000 180.0000 -0.0481
8 CA1 CX 3 7 6 5 1.4950 128.0000 180.0000 -0.1881
9 HA1 HE E 8 7 6 1.1000 109.5000 -30.0000 0.0719
10 HA2 HE E 8 7 6 1.1000 109.5000 -150.0000 0.0719
11 CA2 CY 3 8 7 6 1.5060 109.5000 90.0000 -0.0403
12 HE1 HN E 11 8 7 1.1000 109.5000 180.0000 0.0719
13 HE2 HN E 11 8 7 1.1000 109.5000 300.0000 0.0719
14 HE3 HN E 11 8 7 1.1000 109.5000 60.0000 0.0719
15 C3A CB B 7 6 5 1.3460 106.5000 0.0000 -0.0481
16 CA3 CX 3 15 7 6 1.4950 125.5000 180.0000 -0.1881
17 HA3 HE E 16 15 7 1.1000 109.5000 -30.0000 0.0719
18 HA4 HE E 16 15 7 1.1000 109.5000 -150.0000 0.0719
19 CA4 CY 3 16 15 7 1.5060 109.5000 90.0000 -0.0403
20 HE4 HN E 19 16 15 1.1000 109.5000 180.0000 0.0719
21 HE5 HN E 19 16 15 1.1000 109.5000 300.0000 0.0719
22 HE6 HN E 19 16 15 1.1000 109.5000 60.0000 0.0719
23 C4A CC S 15 7 6 1.4430 106.5000 0.0000 0.0019
24 CHB CD S 23 15 7 1.3710 124.1000 180.0000 -0.1381
25 HHB HM E 24 23 15 1.0900 117.5000 0.0000 0.1219
26 NB NO S 4 3 2 1.9580 90.0000 180.0000 -0.2081
27 C1B CC S 26 4 3 1.3760 128.0000 -90.0000 0.0019
28 C2B CB B 27 26 4 1.4430 111.5000 180.0000 -0.0481
29 CB1 CX 3 28 27 26 1.4950 128.0000 180.0000 -0.1881
30 HB1 HE E 29 28 27 1.1000 109.5000 30.0000 0.0719
31 HB2 HE E 29 28 27 1.1000 109.5000 150.0000 0.0719
32 CB2 CY 3 29 28 27 1.5060 109.5000 -90.0000 -0.0403
33 HF1 HN E 32 28 27 1.1000 109.5000 180.0000 0.0719
34 HF2 HN E 32 28 27 1.1000 109.5000 300.0000 0.0719
35 HF3 HN E 32 28 27 1.1000 109.5000 60.0000 0.0719
36 C3B CB B 28 27 26 1.3460 106.5000 0.0000 -0.0481
37 CB3 CX 3 36 28 27 1.4950 125.5000 180.0000 -0.1881
38 HB3 HE E 37 36 28 1.1000 109.5000 30.0000 0.0719
39 HB4 HE E 28 36 28 1.1000 109.5000 150.0000 0.0719
40 CB4 CY 3 37 36 28 1.5060 109.5000 -90.0000 -0.0403
41 HF4 HN E 40 37 36 1.1000 109.5000 180.0000 0.0719
42 HF5 HN E 40 37 36 1.1000 109.5000 300.0000 0.0719
43 HF6 HN E 40 37 36 1.1000 109.5000 60.0000 0.0719
44 C4B CC S 36 28 27 1.4430 106.5000 0.0000 0.0019
45 CHC CD S 44 36 28 1.3710 124.1000 180.0000 -0.1381
46 HHC HM E 45 44 36 1.0900 117.5000 0.0000 0.1219
47 NC NP S 4 3 2 1.9580 90.0000 270.0000 -0.2081
48 C1C CC S 47 4 3 1.3760 128.0000 -90.0000 0.0019
49 C2C CB B 48 47 4 1.4430 111.5000 180.0000 -0.0481
50 CC1 CX 3 49 48 47 1.4950 128.0000 180.0000 -0.1881
51 HC1 HE E 50 49 48 1.1000 109.5000 -30.0000 0.0719
52 HC2 HE E 50 49 48 1.1000 109.5000 -150.0000 0.0719
53 CC2 CY 3 50 49 48 1.5060 109.5000 90.0000 -0.0403
54 HG1 HN E 53 50 49 1.1000 109.5000 180.0000 0.0719
55 HG2 HN E 53 50 49 1.1000 109.5000 300.0000 0.0719
56 HG3 HN E 53 50 49 1.1000 109.5000 60.0000 0.0719
57 C3C CB B 49 48 47 1.3460 106.5000 0.0000 -0.0481
58 CC3 CX 3 57 49 48 1.4950 125.5000 180.0000 -0.1881
59 HC3 HE E 58 57 49 1.1000 109.5000 -30.0000 0.0719
60 HC4 HE E 58 57 49 1.1000 109.5000 -150.0000 0.0719
61 CC4 CY 3 58 57 49 1.5060 109.5000 90.0000 -0.0403
62 HG4 HN E 61 58 57 1.1000 109.5000 180.0000 0.0719
63 HG5 HN E 61 58 57 1.1000 109.5000 300.0000 0.0719
64 HG6 HN E 61 58 57 1.1000 109.5000 60.0000 0.0719
65 C4C CC S 57 49 48 1.4430 106.5000 0.0000 0.0019
66 CHD CD S 65 57 49 1.3710 124.1000 180.0000 -0.1381
67 HHD HM E 66 65 57 1.0900 117.5000 0.0000 0.1219
68 ND NO S 4 3 2 1.9580 90.0000 360.0000 -0.2081
69 C1D CC S 68 4 3 1.3760 128.0000 -90.0000 0.0019
70 C2D CB B 69 68 4 1.4430 111.5000 180.0000 -0.0481
71 CD1 CX 3 70 69 68 1.4950 128.0000 180.0000 -0.1881
72 HD1 HE E 71 70 69 1.1000 109.5000 30.0000 0.0719
73 HD2 HE E 71 70 69 1.1000 109.5000 150.0000 0.0719
74 CD2 CY 3 71 70 69 1.5060 109.5000 -90.0000 -0.0403
75 HJ1 HN E 74 71 70 1.1000 109.5000 180.0000 0.0719
76 HJ2 HN E 74 71 70 1.1000 109.5000 300.0000 0.0719
77 HJ3 HN E 74 71 70 1.1000 109.5000 60.0000 0.0719
78 C3D CB B 70 69 68 1.3460 106.5000 0.0000 -0.0481
79 CD3 CX 3 78 70 69 1.4950 125.5000 180.0000 -0.1881
80 HD3 HE E 79 78 70 1.1000 109.5000 30.0000 0.0719
81 HD4 HE E 79 78 70 1.1000 109.5000 150.0000 0.0719
82 CD4 CY 3 79 78 70 1.5060 109.5000 -90.0000 -0.0403
83 HJ4 HN E 82 79 78 1.1000 109.5000 180.0000 0.0719
84 HJ5 HN E 82 79 78 1.1000 109.5000 300.0000 0.0719
85 HJ6 HN E 82 79 78 1.1000 109.5000 60.0000 0.0719
86 C4D CC S 78 70 69 1.4430 106.5000 0.0000 0.0019
87 CHA CD S 87 78 70 1.3710 124.1000 180.0000 -0.1381
88 HHA HM E 88 87 78 1.0900 117.5000 0.0000 0.1219
LOOP EXPLICIT
NA C4A
NB C4B
NC C4C
ND C4D
CHB C1B
CHC C1C
CHD C1D
CHA C1A
IMPROPER
C1A CHA HHA C4D
C1B CHB HHB C4A
C1C CHC HHC C4B
C1D CHD HHD C4C
C1A NA NI C4A
C1B NB NI C4B
C1C NC NI C4C
C1D ND NI C4D
C2A C3A CA3 C4A
C2B C3B CB3 C4B
C2C C3C CC3 C4C
C2D C3D CD3 C4D
C1A C2A CA1 C3A
C1B C2B CB1 C3B
C1C C2C CC1 C3C
C1D C2D CD1 C3D
C1B NB CHB C2B
C1C NC CHC C2C
C1D ND CHD C2D
C1A NA CHA C2A
DONE
STOP
0 0 2
united ethyl (cz) nioep
por_beg.db3
POR INT 1
CORRECT NOMIT DU BEG
0.00000
1 DUMM DU M 0 -1 -2 0.0000 0.0000 0.0000 0.0000
2 DUMM DU M 1 0 -1 1.0000 0.0000 0.0000 0.0000
3 DUMM DU M 2 1 0 1.0000 90.0000 0.0000 0.0000
4 NI NI M 3 2 1 2.1100 90.0000 90.0000 0.2500
5 NA NP S 4 3 2 1.9580 90.0000 90.0000 -0.1800
6 C1A CC S 5 4 3 1.3760 128.0000 -90.0000 0.0300
7 C2A CB B 6 5 4 1.4430 111.5000 180.0000 -0.0200
8 HA2 CZ E 7 6 5 1.4950 128.0000 180.0000 0.0288
9 C3A CB B 7 6 5 1.3460 106.5000 0.0000 -0.0200
10 HA3 CZ E 9 7 6 1.4950 125.5000 180.0000 0.0288
11 C4A CC S 9 7 6 1.4430 106.5000 0.0000 0.0300
12 CHB CD S 11 9 7 1.3710 124.1000 180.0000 -0.1100
13 HHB HM E 12 11 9 1.0900 117.5000 0.0000 0.1500
14 NB NO S 4 3 2 1.9580 90.0000 180.0000 -0.1800
15 C1B CC S 14 4 3 1.3760 128.0000 -90.0000 0.0300
16 C2B CB B 15 14 4 1.4430 111.5000 180.0000 -0.0200
17 HB2 CZ E 16 15 14 1.4950 128.0000 180.0000 0.0288
18 C3B CB B 16 15 14 1.3460 106.5000 0.0000 -0.0200
19 HB3 CZ E 18 16 15 1.4950 125.5000 180.0000 0.0288
20 C4B CC S 18 16 15 1.4430 106.5000 0.0000 0.0300
21 CHC CD S 20 18 16 1.3710 124.1000 180.0000 -0.1100
22 HHC HM E 21 20 18 1.0900 117.5000 0.0000 0.1500
23 NC NP S 4 3 2 1.9580 90.0000 270.0000 -0.1800
24 C1C CC S 23 4 3 1.3760 128.0000 -90.0000 0.0300
25 C2C CB B 24 23 4 1.4430 111.5000 180.0000 -0.0200
26 HC2 CZ E 25 24 23 1.4950 128.0000 180.0000 0.0288
27 C3C CB B 25 24 23 1.3460 106.5000 0.0000 -0.0200
28 HC3 CZ E 27 25 24 1.4950 125.5000 180.0000 0.0288
29 C4C CC S 27 25 24 1.4430 106.5000 0.0000 0.0300
30 CHD CD S 29 27 25 1.3710 124.1000 180.0000 -0.1100
31 HHD HM E 30 29 27 1.0900 117.5000 0.0000 0.1500
32 ND NO S 4 3 2 1.9580 90.0000 360.0000 -0.1800
33 C1D CC S 32 4 3 1.3760 128.0000 -90.0000 0.0300
34 C2D CB B 33 32 4 1.4430 111.5000 180.0000 -0.0200
35 HD2 CZ E 34 33 32 1.4950 128.0000 180.0000 0.0288
36 C3D CB B 34 33 32 1.3460 106.5000 0.0000 -0.0200
37 HD3 CZ E 36 34 33 1.4950 125.5000 180.0000 0.0288
38 C4D CC S 36 34 33 1.4430 106.5000 0.0000 0.0300
39 CHA CD S 38 36 34 1.3710 124.1000 180.0000 -0.1100
40 HHA HM E 39 38 36 1.0900 117.5000 0.0000 0.1500
LOOP EXPLICIT
NA C4A
NB C4B
NC C4C
ND C4D
CHB C1B
CHC C1C
CHD C1D
CHA C1A
IMPROPER
C1A CHA HHA C4D
C1B CHB HHB C4A
C1C CHC HHC C4B
C1D CHD HHD C4C
C1A NA NI C4A
C1B NB NI C4B
C1C NC NI C4C
C1D ND NI C4D
C2A C3A HA3 C4A
C2B C3B HB3 C4B
C2C C3C HC3 C4C
C2D C3D HD3 C4D
C1A C2A HA2 C3A
C1B C2B HB2 C3B
C1C C2C HC2 C3C
C1D C2D HD2 C3D
C1B NB CHB C2B
C1C NC CHC C2C
C1D ND CHD C2D
C1A NA CHA C2A
DONE
STOP
HEADER Benzene pdb file
ATOM 1 C1 TOL 1 -0.704 -1.218 0.000
ATOM 2 H1 TOL 1 -1.244 -2.154 0.000
ATOM 3 C2 TOL 1 0.704 -1.218 0.000
ATOM 4 H2 TOL 1 1.244 -2.154 0.000
ATOM 5 C3 TOL 1 1.406 0.000 0.000
ATOM 6 H3 TOL 1 2.488 0.000 0.000
ATOM 7 C4 TOL 1 0.704 1.218 0.000
ATOM 8 H4 TOL 1 1.244 2.154 0.000
ATOM 9 C5 TOL 1 -0.704 1.218 0.000
ATOM 10 H5 TOL 1 -1.244 2.155 0.000
ATOM 11 C6 TOL 1 -1.406 0.000 0.000
ATOM 12 H6 TOL 1 -2.488 0.000 0.000
HEADER Rotated on 27-Jan-97 about 11 12 1
ATOM 1 C1 TOL 1 -0.708 1.218 0.000
ATOM 2 H1 TOL 1 -0.176 2.157 0.017
ATOM 3 C2 TOL 1 -2.114 1.217 -0.038
ATOM 4 H2 TOL 1 -2.654 2.153 -0.042
ATOM 5 C3 TOL 1 -2.817 0.000 -0.071
ATOM 6 H3 TOL 1 -3.898 -0.001 -0.099
ATOM 7 C4 TOL 1 -2.113 -1.217 -0.068
ATOM 8 H4 TOL 1 -2.652 -2.153 -0.095
ATOM 9 C5 TOL 1 -0.707 -1.217 -0.031
ATOM 10 H5 TOL 1 -0.174 -2.158 -0.036
ATOM 11 C6 TOL 1 0.000 0.000 0.000
ATOM 12 C7 TOL 1 1.517 0.000 0.000
ATOM 13 C8 TOL 1 2.121 0.003 -1.406
ATOM 14 H81 TOL 1 1.791 -0.883 -1.949
ATOM 15 H82 TOL 1 1.793 0.893 -1.944
ATOM 16 H83 TOL 1 3.209 0.001 -1.340
ATOM 17 H72 TOL 1 1.871 -0.882 0.536
ATOM 18 H73 TOL 1 1.873 0.877 0.541
HEADER Myoglobin Heme pdb file
ATOM 1491 N HEM 93 -0.269 -2.440 -6.103
ATOM 1492 HN HEM 93 0.400 -1.686 -6.171
ATOM 1493 CA HEM 93 -1.636 -2.086 -5.787
ATOM 1494 HA HEM 93 -1.971 -2.732 -4.975
ATOM 1495 CB HEM 93 -1.731 -0.554 -5.390
ATOM 1496 HB2 HEM 93 -1.354 0.028 -6.232
ATOM 1497 HB3 HEM 93 -2.776 -0.268 -5.279
ATOM 1498 CG HEM 93 -1.016 -0.204 -4.092
ATOM 1499 ND1 HEM 93 0.241 -0.644 -3.788
ATOM 1500 HND HEM 93 0.917 -1.056 -4.416
ATOM 1501 CE1 HEM 93 0.560 -0.404 -2.517
ATOM 1502 HE HEM 93 1.571 -0.564 -2.172
ATOM 1503 NE2 HEM 93 -0.476 0.000 -1.825
ATOM 1504 CD2 HEM 93 -1.443 0.272 -2.878
ATOM 1505 HD HEM 93 -2.466 0.485 -2.605
ATOM 1506 FE HEM 93 -0.502 0.394 0.422
ATOM 1507 NA HEM 93 1.492 0.125 0.462
ATOM 1508 C1A HEM 93 2.194 -1.018 0.713
ATOM 1509 C2A HEM 93 3.622 -0.722 0.477
ATOM 1510 CAA HEM 93 4.750 -1.790 0.532
ATOM 1511 HP71HEM 93 5.564 -1.177 0.919
ATOM 1512 HP72HEM 93 4.540 -2.626 1.198
ATOM 1513 CBA HEM 93 5.219 -2.336 -0.914
ATOM 1514 HP73HEM 93 6.205 -2.772 -0.754
ATOM 1515 HP74HEM 93 5.174 -1.515 -1.629
ATOM 1516 CGA HEM 93 4.196 -3.421 -1.409
ATOM 1517 O1A HEM 93 3.275 -2.972 -2.119
ATOM 1518 O2A HEM 93 4.072 -4.496 -0.753
ATOM 1519 C3A HEM 93 3.833 0.621 0.242
ATOM 1520 CMA HEM 93 5.022 1.287 -0.284
ATOM 1521 HM81HEM 93 5.289 1.005 -1.302
ATOM 1522 HM82HEM 93 4.905 2.370 -0.245
ATOM 1523 HM83HEM 93 5.924 1.004 0.259
ATOM 1524 C4A HEM 93 2.492 1.120 0.203
ATOM 1525 CHB HEM 93 2.140 2.473 -0.090
ATOM 1526 HDM HEM 93 2.972 3.145 -0.303
ATOM 1527 C1B HEM 93 0.909 3.069 -0.098
ATOM 1528 NB HEM 93 -0.227 2.400 0.178
ATOM 1529 C2B HEM 93 0.625 4.446 -0.295
ATOM 1530 CMB HEM 93 1.682 5.549 -0.260
ATOM 1531 HM11HEM 93 2.340 5.438 -1.122
ATOM 1532 HM12HEM 93 1.320 6.517 -0.606
ATOM 1533 HM13HEM 93 2.146 5.747 0.706
ATOM 1534 C3B HEM 93 -0.760 4.554 -0.275
ATOM 1535 CAB HEM 93 -1.487 5.930 -0.240
ATOM 1537 CBB HEM 93 -1.115 7.013 0.373
ATOM 1538 HV2CHEM 93 -0.292 6.991 1.071
ATOM 1539 HV2THEM 93 -1.726 7.872 0.136
ATOM 1540 C4B HEM 93 -1.257 3.250 -0.160
ATOM 1541 CHC HEM 93 -2.606 2.942 -0.222
ATOM 1542 HAM HEM 93 -3.421 3.652 -0.365
ATOM 1543 C1C HEM 93 -3.208 1.687 0.041
ATOM 1544 NC HEM 93 -2.460 0.548 0.302
ATOM 1545 C2C HEM 93 -4.621 1.487 0.183
ATOM 1546 CMC HEM 93 -5.704 2.459 0.255
ATOM 1547 HM31HEM 93 -6.688 2.105 0.563
ATOM 1548 HM32HEM 93 -5.339 3.197 0.969
ATOM 1549 HM33HEM 93 -5.818 2.960 -0.706
ATOM 1550 C3C HEM 93 -4.715 0.147 0.398
ATOM 1551 CAC HEM 93 -5.949 -0.672 0.686
ATOM 1553 CBC HEM 93 -6.961 -0.270 1.527
ATOM 1554 HV4CHEM 93 -6.927 0.642 2.105
ATOM 1555 HV4THEM 93 -7.796 -0.941 1.668
ATOM 1556 C4C HEM 93 -3.425 -0.428 0.350
ATOM 1557 CHD HEM 93 -3.160 -1.811 0.542
ATOM 1558 HBM HEM 93 -4.032 -2.425 0.766
ATOM 1559 C1D HEM 93 -1.921 -2.354 0.535
ATOM 1560 ND HEM 93 -0.741 -1.591 0.704
ATOM 1561 C2D HEM 93 -1.745 -3.778 0.850
ATOM 1562 CMD HEM 93 -2.900 -4.814 1.017
ATOM 1563 HM51HEM 93 -3.333 -4.981 0.030
ATOM 1564 HM52HEM 93 -2.618 -5.815 1.344
ATOM 1565 HM53HEM 93 -3.696 -4.437 1.660
ATOM 1566 C3D HEM 93 -0.419 -3.859 1.220
ATOM 1567 C4D HEM 93 0.203 -2.532 1.084
ATOM 1568 CHA HEM 93 1.585 -2.245 1.001
ATOM 1569 HGM HEM 93 2.245 -3.091 1.192
ATOM 1570 CAD HEM 93 0.326 -5.056 1.650
ATOM 1571 HP61HEM 93 -0.119 -5.991 1.311
ATOM 1572 HP62HEM 93 1.361 -4.981 1.315
ATOM 1573 CBD HEM 93 0.313 -5.184 3.204
ATOM 1574 HP63HEM 93 -0.679 -5.068 3.640
ATOM 1575 HP64HEM 93 0.409 -6.255 3.379
ATOM 1576 CGD HEM 93 1.461 -4.568 3.968
ATOM 1577 O1D HEM 93 1.356 -4.243 5.168
ATOM 1578 O2D HEM 93 2.609 -4.691 3.539
ATOM 1579 CMX HEM 93 -0.380 0.955 2.493
ATOM 1580 OMX HEM 93 -0.229 1.303 3.552
ATOM 1581 C HEM 93 -2.567 -2.364 -6.942
ATOM 1582 O HEM 93 -3.777 -2.509 -6.766
Nickel octa ethyl porphine PDB File
HEADER starting coordinates nioep full
ATOM 1 NI POR 1 0.000 0.000 0.000
ATOM 2 NA POR 1 1.965 0.000 0.010
ATOM 3 C1A POR 1 2.813 -1.083 0.014
ATOM 4 C2A POR 1 4.210 -0.678 0.020
ATOM 5 CA1 POR 1 5.412 -1.602 0.046
ATOM 6 HA1 POR 1 5.191 -2.479 0.671
ATOM 7 HA2 POR 1 6.276 -1.093 0.494
ATOM 8 CA2 POR 1 5.763 -2.047 -1.355
ATOM 9 HE1 POR 1 6.630 -2.724 -1.321
ATOM 10 HE2 POR 1 4.911 -2.577 -1.807
ATOM 11 HE3 POR 1 6.013 -1.176 -1.978
ATOM 12 C3A POR 1 4.210 0.678 0.020
ATOM 13 CA3 POR 1 5.412 1.602 0.046
ATOM 14 HA3 POR 1 6.276 1.093 0.494
ATOM 15 HA4 POR 1 5.191 2.479 0.671
ATOM 16 CA4 POR 1 5.763 2.047 -1.355
ATOM 17 HE4 POR 1 6.630 2.724 -1.321
ATOM 18 HE5 POR 1 6.013 1.176 -1.978
ATOM 19 HE6 POR 1 4.911 2.577 -1.807
ATOM 20 C4A POR 1 2.813 1.083 0.014
ATOM 21 CHB POR 1 2.400 2.400 0.000
ATOM 22 HHB POR 1 3.167 3.167 0.000
ATOM 23 NB POR 1 0.000 1.965 -0.010
ATOM 24 C1B POR 1 1.083 2.813 -0.014
ATOM 25 C2B POR 1 0.678 4.210 -0.020
ATOM 26 CB1 POR 1 1.602 5.412 -0.046
ATOM 27 HB1 POR 1 2.479 5.191 -0.671
ATOM 28 HB2 POR 1 1.093 6.276 -0.494
ATOM 29 CB2 POR 1 2.047 5.763 1.355
ATOM 30 HF1 POR 1 2.724 6.630 1.321
ATOM 31 HF2 POR 1 1.176 6.013 1.978
ATOM 32 HF3 POR 1 2.577 4.911 1.807
ATOM 33 C3B POR 1 -0.678 4.210 -0.020
ATOM 34 CB3 POR 1 -1.602 5.412 -0.046
ATOM 35 HB3 POR 1 -1.093 6.276 -0.494
ATOM 36 HB4 POR 1 -2.479 5.191 -0.671
ATOM 37 CB4 POR 1 -2.047 5.763 1.355
ATOM 38 HF4 POR 1 -2.724 6.630 1.321
ATOM 39 HF5 POR 1 -2.577 4.911 1.807
ATOM 40 HF6 POR 1 -1.176 6.013 1.978
ATOM 41 C4B POR 1 -1.083 2.813 -0.014
ATOM 42 CHC POR 1 -2.400 2.400 0.000
ATOM 43 HHC POR 1 -3.167 3.167 0.000
ATOM 44 NC POR 1 -1.965 0.000 0.010
ATOM 45 C1C POR 1 -2.813 1.083 0.014
ATOM 46 C2C POR 1 -4.210 0.678 0.020
ATOM 47 CC1 POR 1 -5.412 1.602 0.046
ATOM 48 HC1 POR 1 -5.191 2.479 0.671
ATOM 49 HC2 POR 1 -6.276 1.093 0.494
ATOM 50 CC2 POR 1 -5.763 2.047 -1.355
ATOM 51 HG1 POR 1 -6.630 2.724 -1.321
ATOM 52 HG2 POR 1 -4.911 2.577 -1.807
ATOM 53 HG3 POR 1 -6.013 1.176 -1.978
ATOM 54 C3C POR 1 -4.210 -0.678 0.020
ATOM 55 CC3 POR 1 -5.412 -1.602 0.046
ATOM 56 HC3 POR 1 -6.276 -1.093 0.494
ATOM 57 HC4 POR 1 -5.191 -2.479 0.671
ATOM 58 CC4 POR 1 -5.763 -2.047 -1.355
ATOM 59 HG4 POR 1 -6.630 -2.724 -1.321
ATOM 60 HG5 POR 1 -6.013 -1.176 -1.978
ATOM 61 HG6 POR 1 -4.911 -2.577 -1.807
ATOM 62 C4C POR 1 -2.813 -1.083 0.014
ATOM 63 CHD POR 1 -2.400 -2.400 0.000
ATOM 64 HHD POR 1 -3.167 -3.167 0.000
ATOM 65 ND POR 1 0.000 -1.965 -0.010
ATOM 66 C1D POR 1 -1.083 -2.813 -0.014
ATOM 67 C2D POR 1 -0.678 -4.210 -0.020
ATOM 68 CD1 POR 1 -1.602 -5.412 -0.046
ATOM 69 HD1 POR 1 -2.479 -5.191 -0.671
ATOM 70 HD2 POR 1 -1.093 -6.276 -0.494
ATOM 71 CD2 POR 1 -2.047 -5.763 1.355
ATOM 72 HJ1 POR 1 -2.724 -6.630 1.321
ATOM 73 HJ2 POR 1 -1.176 -6.013 1.978
ATOM 74 HJ3 POR 1 -2.577 -4.911 1.807
ATOM 75 C3D POR 1 0.678 -4.210 -0.020
ATOM 76 CD3 POR 1 1.602 -5.412 -0.046
ATOM 77 HD3 POR 1 1.093 -6.276 -0.494
ATOM 78 HD4 POR 1 2.479 -5.191 -0.671
ATOM 79 CD4 POR 1 2.047 -5.763 1.355
ATOM 80 HJ4 POR 1 2.724 -6.630 1.321
ATOM 81 HJ5 POR 1 2.577 -4.911 1.807
ATOM 82 HJ6 POR 1 1.176 -6.013 1.978
ATOM 83 C4D POR 1 1.083 -2.813 -0.014
ATOM 84 CHA POR 1 2.400 -2.400 0.000
ATOM 85 HHA POR 1 3.167 -3.167 0.000
HEADER Symmetric coordinates Nipor Jason's
ATOM 1 NI POR 1 0.000 0.000 0.000
ATOM 2 NB POR 1 0.000 1.974 0.000
ATOM 3 C1B POR 1 1.099 2.821 0.000
ATOM 4 C2B POR 1 0.675 4.202 0.000
ATOM 5 CHB POR 1 2.435 2.435 0.000
ATOM 6 HB2 POR 1 1.319 5.070 0.000
ATOM 7 HHB POR 1 3.199 3.199 0.000
ATOM 8 NA POR 1 1.974 0.000 0.000
ATOM 9 ND POR 1 0.000 -1.974 0.000
ATOM 10 NC POR 1 -1.974 0.000 0.000
ATOM 11 C4A POR 1 2.821 1.099 0.000
ATOM 12 C1A POR 1 2.821 -1.099 0.000
ATOM 13 C4D POR 1 1.099 -2.821 0.000
ATOM 14 C1D POR 1 -1.099 -2.821 0.000
ATOM 15 C4C POR 1 -2.821 -1.099 0.000
ATOM 16 C1C POR 1 -2.821 1.099 0.000
ATOM 17 C4B POR 1 -1.099 2.821 0.000
ATOM 18 C3A POR 1 4.202 0.675 0.000
ATOM 19 C2A POR 1 4.202 -0.675 0.000
ATOM 20 C3D POR 1 0.675 -4.202 0.000
ATOM 21 C2D POR 1 -0.675 -4.202 0.000
ATOM 22 C3C POR 1 -4.202 -0.675 0.000
ATOM 23 C2C POR 1 -4.202 0.675 0.000
ATOM 24 C3B POR 1 -0.675 4.202 0.000
ATOM 25 CHA POR 1 2.435 -2.435 0.000
ATOM 26 CHD POR 1 -2.435 -2.435 0.000
ATOM 27 CHC POR 1 -2.435 2.435 0.000
ATOM 28 HA3 POR 1 5.070 1.319 0.000
ATOM 29 HA2 POR 1 5.070 -1.319 0.000
ATOM 30 HD3 POR 1 1.319 -5.070 0.000
ATOM 31 HD2 POR 1 -1.319 -5.070 0.000
ATOM 32 HC3 POR 1 -5.070 -1.319 0.000
ATOM 33 HC2 POR 1 -5.070 1.319 0.000
ATOM 34 HB3 POR 1 -1.319 5.070 0.000
ATOM 35 HHA POR 1 3.199 -3.199 0.000
ATOM 36 HHD POR 1 -3.199 -3.199 0.000
ATOM 37 HHC POR 1 -3.199 3.199 0.000
Relative Scale Factors for Improper Torsions

Vdih = f(1,2)Vn(1+cos(n[[phi]]-[[gamma]]))
The above set of atoms A-C-D-B is associated with an improper torsion hinged
about the bond
C-D. The relative scaling factor between Vn/2 choosen for
different hinge atoms is given by the following ratios:
Vdih' = Vn/2'(1+cos(n[[phi]]'-[[gamma]])) = Vdih =Vn/2(1+cos(n[[phi]]-[[gamma]]))
or
Vn/2 = Vn/2' f((1+cos(n[[phi]]'-[[gamma]])),(1+cos(n[[phi]]-[[gamma]])))
The relative scaling factor between Spiro's wagging force constants defined in terms of [[theta]] and the Amber torsion constants defined in terms of [[phi]] are given by the following ratios:
Vdih = Vn/2(1+cos(n[[phi]]-[[gamma]])) = Vpln = f(1,2) k[[theta]] [[theta]]2
or
Vn/2 = k[[theta]] f([[theta]]2,2(1+cos(n[[phi]]-[[gamma]])))
The relative scaling factor between Karplus force constants defined in terms of [[phi]] and the Amber torsion constants defined in terms of [[phi]] are given by the following ratios:
Vdih = Vn/2(1+cos(n[[phi]]-[[gamma]])) = Vang = f(1,2) k[[phi]] [[phi]]2
or
Vn/2 = k[[phi]] f([[phi]]2,2(1+cos(n[[phi]]-[[gamma]])))
Since k[[phi]] = d2Vdih/d[[phi]]2 = n2 Vn/2; emplies Vn/2 = f(k[[phi]],n2) or a factor of .25 for n=2.
The following program used as input the pdb coordinates of heme, and a set of integers contained in namelist start in file cntrl defining respectively the four atoms of the improper torsion (A,B,C,D), the atom which is wagging (D) and the atom to which the wagging atom is attached(C).
Resultes from dihtest2
dihtest2 -c cntrl < pdbout
$start
nstep = 3
step = 0.1000000
norder = 2
gamma = 180.0000
rk = 100.0000
vn2 = 25.00000
$end
1 Ni pucker = 11 1 2 29 1 2
2 Ni wag = 3 1 2 8 1 2
3 Ni wag = 1 3 8 2 1 2
4 Ni wag = 8 3 1 2 1 2
5 Cz wag = 3 4 5 6 5 4
6 Cz wag = 4 3 6 5 5 4
7 Cz wag = 4 3 5 6 5 4
8 Hm wag = 3 36 37 35 37 36
9 Hm wag = 36 3 35 37 37 36
10 Hm wag = 36 3 37 35 37 36
11 Hm wag = 37 3 36 35 37 36
12 Cm pucker = 3 36 37 35 36 37
13 Cm pucker = 36 3 35 37 36 37
14 Cm pucker = 36 3 37 35 36 37
15 Ca pucker = 3 2 4 36 2 36
16 Ca pucker = 3 36 4 2 2 36
17 Ca pucker = 3 36 2 4 2 36
18 Ca pucker = 36 2 3 4 2 36
19 Ca pucker = 36 2 4 3 2 36
20 Ca pucker = 3 2 36 4 2 36
................. CB3 .......... CB2 .............
. .
. .
. C3B C2B .
. .
. HHC HHB .
. C4B C1B .
. CHC CHB .
. NB .
CC2 CA3
. C1C C4A .
. C2C C3A .
. .
. NC NI NA .
. C3C C2A .
. C4C C1A .
CC3 CA2
. ND .
. CHD CHA .
. C1D C4D .
. HHD HHA .
. .
. C2D C3D .
. .
. .
................. CD2 .......... CD3 .............
1=NI 2= NA 3= C1A 4= C2A 5= CA2
6= C3A 7= CA3 8= C4A 9= CHB 10= HHB
11= NB 12= C1B 13= C2B 14= CB2 15= C3B
16= CB3 17= C4B 18= CHC 19= HHC 20= NC
21= C1C 22= C2C 23= CC2 24= C3C 25= CC3
26= C4C 27= CHD 28= HHD 29= ND 30= C1D
31= C2D 32= CD2 33= C3D 34= CD3 35= C4D
36= CHA 37= HHA
V dih = 2*(1+cos(n*ang-gamma))
V pln= (angle to plane)**2
V ang= ang**2
Use the V dih to tell relative strenghts
Use the ang/dih to tell strenghts of karplus
Use the pln/dih to tell strenghts of spiro
# NB -NI - NA - ND with NI === Ni pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 5.828 2.918 0.0412 0.0026 0.0103 0.0629 0.2509
0.20 11.581 5.820 0.1612 0.0103 0.0409 0.0640 0.2534
# C1A-NI - NA - C4A with NI === Ni wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 4.556 2.918 0.0252 0.0026 0.0063 0.1028 0.2505
0.20 9.062 5.820 0.0992 0.0103 0.0250 0.1040 0.2521
#NI - C1A- C4A- NA with NI === Ni wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 2.036 2.918 0.0050 0.0026 0.0013 0.5137 0.2501
0.20 4.067 5.820 0.0201 0.0103 0.0050 0.5130 0.2504
# C4A- C1A-NI - NA with NI === Ni wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 2.442 2.918 0.0073 0.0026 0.0018 0.3570 0.2501
0.20 4.858 5.820 0.0287 0.0103 0.0072 0.3597 0.2506
# C1A- C2A- CA2- C3A with CA2=== Cz wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 5.665 3.811 0.0390 0.0044 0.0098 0.1136 0.2508
0.20 11.228 7.589 0.1516 0.0175 0.0384 0.1157 0.2532
# C2A- C1A- C3A- CA2 with CA2=== Cz wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.028 0.000 0.0000 0.0000 0.0000 0.0000 0.2500
0.10 2.454 3.811 0.0073 0.0044 0.0018 0.6033 0.2502
0.20 4.899 7.589 0.0292 0.0175 0.0073 0.6013 0.2506
# C2A- C1A- CA2- C3A with CA2=== Cz wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 3.094 3.811 0.0117 0.0044 0.0029 0.3798 0.2502
0.20 6.130 7.589 0.0456 0.0175 0.0114 0.3847 0.2510
# C1A- CHA- HHA- C4D with HHA=== Hm wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 5.527 5.247 0.0371 0.0084 0.0093 0.2260 0.2508
0.20 10.893 10.407 0.1429 0.0330 0.0361 0.2309 0.2530
# CHA- C1A- C4D- HHA with HHA=== Hm wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 3.304 5.247 0.0133 0.0084 0.0033 0.6313 0.2503
0.20 6.585 10.407 0.0526 0.0330 0.0132 0.6271 0.2511
# CHA- C1A- HHA- C4D with HHA=== Hm wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 3.378 5.247 0.0139 0.0084 0.0035 0.6039 0.2503
0.20 6.650 10.407 0.0536 0.0330 0.0135 0.6150 0.2511
# HHA- C1A- CHA- C4D with HHA=== Hm wag ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 5.928 5.247 0.0427 0.0084 0.0107 0.1965 0.2509
0.20 11.732 10.407 0.1654 0.0330 0.0419 0.1995 0.2535
# C1A- CHA- HHA- C4D with CHA=== Cm pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 14.809 5.247 0.2613 0.0084 0.0668 0.0321 0.2556
0.20 28.795 10.407 0.9281 0.0330 0.2526 0.0355 0.2722
# CHA- C1A- C4D- HHA with CHA=== Cm pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 8.834 5.247 0.0943 0.0084 0.0238 0.0889 0.2520
0.20 17.266 10.407 0.3524 0.0330 0.0908 0.0936 0.2577
# CHA- C1A- HHA- C4D with CHA=== Cm pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 9.067 5.247 0.0993 0.0084 0.0250 0.0844 0.2521
0.20 17.701 10.407 0.3698 0.0330 0.0954 0.0892 0.2581
# C1A- NA - C2A- CHA with NA === Ca pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.028 0.000 0.0000 0.0000 0.0000 0.0000 0.2500
0.10 2.334 2.341 0.0066 0.0017 0.0017 0.2516 0.2501
0.20 4.626 4.673 0.0260 0.0067 0.0065 0.2557 0.2505
# C1A- CHA- C2A- NA with NA === Ca pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 2.807 2.341 0.0096 0.0017 0.0024 0.1739 0.2502
0.20 5.601 4.673 0.0381 0.0067 0.0096 0.1746 0.2508
# C1A- CHA- NA - C2A with NA === Ca pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 2.911 2.341 0.0103 0.0017 0.0026 0.1618 0.2502
0.20 5.756 4.673 0.0402 0.0067 0.0101 0.1653 0.2508
# CHA- NA - C1A- C2A with NA === Ca pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 4.487 2.341 0.0245 0.0017 0.0061 0.0682 0.2505
0.20 8.888 4.673 0.0955 0.0067 0.0241 0.0697 0.2520
# CHA- NA - C2A- C1A with NA === Ca pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.000 0.000 0.0000 0.0000 0.0000 -1.0000 -1.0000
0.10 2.334 2.341 0.0066 0.0017 0.0017 0.2516 0.2501
0.20 4.626 4.673 0.0260 0.0067 0.0065 0.2557 0.2505
# C1A- NA - CHA- C2A with NA === Ca pucker ratios
# z angle anglep V dih V pln V ang Vpln/Vdih Vang/Vih
0.00 0.020 0.000 0.0000 0.0000 0.0000 0.0000 0.2499
0.10 2.911 2.341 0.0103 0.0017 0.0026 0.1618 0.2502
0.20 5.756 4.673 0.0402 0.0067 0.0101 0.1653 0.2508
benzene frequencies taken from the Scherer paper.
Symmetry classification done here,charac added 01/15/97
13,'???','a1g','a2g','a1u','a2u','b1g','b2g','b1u','b2u','e1g','e1u','e2g','e2u'/tt>
none
20 1 1 992.0 1.0
20 1 2 3062.0 1.0
30 2 1 1326.0 1.0
40 4 1 673.0 1.0
40 6 1 703.0 1.0
40 6 2 995.0 1.0
30 7 1 1010.0 1.0
20 7 2 3068.0 1.0
0 8 1 1150.0 1.0
0 8 2 1310.0 0.0
40 9 1 849.0 1.0
40 9 2 849.0 1.0
20 10 1 1038.0 1.0
20 10 2 1038.0 1.0
30 10 3 1486.0 1.0
30 10 4 1486.0 1.0
20 10 5 3063.0 1.0
20 10 6 3063.0 1.0
60 11 1 606.0 1.0
60 11 2 606.0 1.0
60 11 3 1178.0 1.0
60 11 4 1178.0 1.0
60 11 5 1596.0 1.0
60 11 6 1596.0 1.0
20 11 7 3047.0 1.0
20 11 8 3047.0 1.0
40 12 1 410.0 1.0
40 12 2 410.0 1.0
40 12 3 975.0 1.0
40 12 4 975.0 1.0
200 0 1 1596.0 0.0
300 0 2 1486.0 0.0
400 0 3 995.0 0.0
Ethylbenzene (Cs sym) with the methyl group version 0
new file taken from ref#
3 "???" "a1 " "a2 "
none
200 0 1 1712.0 0.0
300 0 2 1530.0 0.0
400 0 3 982.0 0.0
0 1 1 152.0 1.0
0 1 2 308.0 1.0
0 1 3 493.0 1.0
0 1 4 557.0 1.0
0 1 5 700.0 1.0
0 1 6 749.0 1.0
0 1 7 771.0 1.0
0 1 8 903.0 1.0
0 1 9 962.0 1.0
40 1 10 990.0 1.0
60 1 11 1005.0 1.0
60 1 12 1021.0 1.0
60 1 13 1065.0 1.0
60 1 14 1183.0 1.0
60 1 15 1207.0 1.0
60 1 16 1321.0 1.0
60 1 17 1378.0 1.0
60 1 18 1455.0 1.0
60 1 19 1467.0 1.0
60 1 20 1500.0 1.0
60 1 21 1606.0 1.0
60 1 22 2900.0 0.0
60 1 23 2949.0 0.0
60 1 24 3055.0 0.0
60 1 25 3056.0 0.0
60 1 26 3056.0 0.0
60 1 27 3057.0 0.0
0 2 1 45.0 0.3
0 2 2 190.0 0.3
0 2 3 360.0 1.0
0 2 4 415.0 1.0
0 2 5 618.0 1.0
0 2 6 787.0 1.0
0 2 7 856.0 1.0
40 2 8 975.0 0.5
60 2 9 1033.0 1.0
60 2 10 1098.0 1.0
60 2 11 1157.0 1.0
60 2 12 1245.0 1.0
60 2 13 1300.0 1.0
60 2 14 1332.0 1.0
60 2 15 1453.0 0.1
60 2 16 1459.0 0.1
60 2 17 1589.0 0.1
60 2 18 2951.0 0.0
60 2 19 3055.0 0.0
60 2 20 3055.0 0.0
60 2 21 3055.0 0.0
Nickel Octa Ethyl Porphine Obs File
nioepun with non-united methyl atoms, freq ordering changed
modified obsfull20
6 "???" "a1 " "a2 " "b1 " "b2 " "e "
none N15 Meso D
40 1 1 30.0 0.00 1 30.0 0.50 1 30.0 0.50
90 1 2 127.0 1.00 2 127.0 1.00 2 127.0 1.00
40 1 3 139.0 0.00 3 139.0 0.00 3 139.0 0.00
0 1 4 200.0 0.00 4 200.0 0.00 4 200.0 0.00
60 1 5 263.0 0.01 5 261.0 0.01 5 262.0 0.01
0 1 6 270.0 0.50 6 268.0 0.50 6 270.0 0.50
60 1 7 360.0 0.01 7 358.0 0.01 7 353.0 0.01
60 1 8 477.0 0.50 8 475.0 0.50 8 477.0 0.50
60 1 9 674.0 1.00 9 671.0 1.00 9 663.0 1.00
40 1 11 704.0 1.00 11 700.0 1.00 11 704.0 1.00
60 1 10 770.0 1.00 10 769.0 1.00 10 776.0 1.00
60 1 12 804.0 1.00 12 799.0 1.00 12 799.0 1.00
0 1 13 927.0 0.00 13 927.0 0.00 13 927.0 0.00
60 1 14 979.0 0.00 14 979.0 0.00 14 979.0 0.00
60 1 15 1024.0 10.00 15 1021.0 1.00 15 1024.0 1.00
60 1 16 1138.0 1.00 16 1131.0 1.00 16 1138.0 1.00
60 1 17 1258.0 1.00 17 1257.0 1.00 17 1258.0 1.00
60 1 18 1316.0 1.00 18 1316.0 1.00 18 1316.0 1.00
60 1 19 1378.0 0.00 19 1378.0 0.00 19 1378.0 0.00
60 1 20 1383.0 1.00 20 1376.0 1.00 20 1382.0 1.00
0 1 21 1400.0 0.00 21 1400.0 0.00 21 1400.0 0.00
60 1 22 1464.0 1.00 22 1464.0 1.00 22 1464.0 1.00
60 1 23 1520.0 1.00 23 1519.0 1.00 23 1512.0 1.00
60 1 24 1602.0 1.00 24 1601.0 1.00 24 1601.0 1.00
60 1 27 2941.0 0.00 27 2941.0 0.00 27 2941.0 0.00
60 1 28 2941.0 0.00 28 2941.0 0.00 28 2941.0 0.00
60 1 31 3041.0 0.50 31 3041.0 0.50 31 2263.0 0.50
40 2 1 44.0 0.00 1 44.0 0.00 1 43.0 0.00
40 2 2 60.0 0.00 2 60.0 0.00 2 60.0 0.00
90 2 3 130.0 0.00 3 130.0 0.00 3 125.0 0.50
0 2 4 200.0 0.00 4 200.0 0.00 4 200.0 0.00
60 2 5 243.0 0.00 5 243.0 0.00 5 243.0 0.00
60 2 6 392.0 0.01 6 392.0 0.01 6 392.0 0.01
60 2 7 551.0 1.00 7 551.0 1.00 7 545.0 1.00
60 2 9 597.0 0.50 9 594.0 0.50 9 582.0 0.50
40 2 8 612.0 25.00 8 612.0 25.00 8 652.0 25.00
40 2 10 732.0 0.25 10 732.0 0.25 10 790.0 0.25
60 2 11 842.0 0.00 11 842.0 0.00 11 842.0 0.00
40 2 12 853.0 0.04 12 853.0 0.04 12 501.0 0.04
0 2 13 931.0 0.00 13 931.0 0.00 13 931.0 0.00
0 2 14 957.0 0.00 14 957.0 0.00 14 957.0 0.00
60 2 15 1014.0 0.00 15 1014.0 0.00 15 1016.0 0.10
60 2 16 1058.0 1.00 16 1058.0 1.00 16 1058.0 1.00
60 2 17 1121.0 1.00 17 1106.0 1.00 17 1202.0 1.00
60 2 18 1252.0 1.00 18 1252.0 1.00 18 1260.0 1.00
60 2 19 1307.0 0.50 19 1303.0 0.50 19 887.0 0.50
60 2 20 1351.0 0.00 20 1351.0 0.00 20 1309.0 0.50
60 2 21 1374.0 0.50 21 1351.0 0.50 21 1309.0 0.50
60 2 22 1393.0 1.00 22 1393.0 1.00 22 1393.0 1.00
0 2 23 1410.0 0.00 23 1410.0 0.00 23 1410.0 0.00
60 2 24 1462.0 1.00 24 1462.0 1.00 24 1461.0 1.00
0 2 25 1562.0 0.00 25 1562.0 0.00 25 1562.0 0.00
60 2 26 1603.0 1.00 26 1602.0 1.00 26 1602.0 1.00
60 2 29 2941.0 0.00 29 2941.0 0.00 29 2965.0 0.00
60 2 31 2941.0 0.00 31 2941.0 0.00 31 2941.0 0.00
40 3 1 74.0 0.00 1 74.0 0.00 1 74.0 0.00
40 3 2 60.0 0.00 2 60.0 0.00 2 60.0 0.00
40 3 3 144.0 0.50 3 144.0 0.50 3 141.0 0.50
60 3 4 197.0 0.50 4 197.0 0.50 4 197.0 0.50
0 3 5 250.0 0.00 5 250.0 0.00 5 250.0 0.00
60 3 6 445.0 5.00 6 445.0 1.00 6 445.0 1.00
40 3 7 346.0 0.00 7 346.0 0.00 7 346.0 0.50
60 3 8 493.0 1.00 8 492.0 1.00 8 490.0 1.00
60 3 9 657.0 0.00 9 657.0 0.00 9 657.0 1.00
60 3 11 938.0 0.50 11 938.0 0.50 11 934.0 0.50
90 3 10 750.0 1.00 10 750.0 1.00 10 750.0 1.00
0 3 12 910.0 0.00 12 910.0 0.00 12 910.0 0.00
60 3 13 1015.0 1.00 13 1006.0 1.00 13 1003.0 1.00
60 3 14 1024.0 0.00 14 1021.0 0.00 14 1031.0 0.00
0 3 15 1100.0 0.00 15 1100.0 0.00 15 1100.0 0.00
60 3 16 1159.0 1.00 16 1149.0 1.00 16 1159.0 1.00
60 3 17 1269.0 0.00 17 1269.0 0.00 17 1269.0 0.00
60 3 18 1350.0 0.00 18 1350.0 0.00 18 1350.0 0.00
0 3 19 1360.0 0.00 19 1360.0 0.00 19 1360.0 0.00
60 3 20 1370.0 0.00 20 1370.0 0.00 20 1370.0 0.00
60 3 21 1407.0 1.00 21 1406.0 1.00 21 1405.0 1.00
60 3 22 1459.0 0.00 22 1459.0 0.00 22 1459.0 0.00
60 3 23 1483.0 1.00 23 1480.0 1.00 23 1478.0 1.00
0 3 24 1583.0 0.00 24 1583.0 0.00 24 1583.0 0.00
60 3 27 2941.0 0.00 27 2941.0 0.00 27 2941.0 0.00
60 3 28 2941.0 0.00 28 2941.0 0.00 28 2941.0 0.00
60 3 30 3041.0 0.50 30 3041.0 0.50 30 2261.0 0.50
40 4 1 32.0 0.00 1 32.0 0.00 1 32.0 0.00
40 4 2 90.0 0.00 2 90.0 0.00 2 90.0 0.00
60 4 3 168.0 1.00 3 168.0 1.00 3 168.0 1.00
90 4 4 108.0 0.00 4 108.0 0.00 4 107.0 0.50
0 4 5 200.0 0.00 5 200.0 0.00 5 200.0 0.00
46 4 6 284.0 1.00 6 284.0 1.00 6 277.0 1.00
60 4 7 305.0 1.00 7 305.0 1.00 7 305.0 1.00
40 4 8 360.0 25.00 8 355.0 25.00 8 337.0 25.00
60 4 9 525.0 10.00 9 525.0 1.00 9 525.0 1.00
60 4 10 740.0 0.01 10 740.0 0.01 10 762.0 0.01
60 4 11 751.0 0.10 11 748.0 0.10 11 683.0 0.10
40 4 12 739.0 4.00 12 733.0 4.00 12 760.0 4.00
60 4 14 781.0 1.00 14 781.0 1.00 14 781.0 1.00
40 4 13 844.0 4.00 13 844.0 4.00 13 681.0 4.00
0 4 15 900.0 0.00 15 900.0 0.00 15 900.0 0.00
60 4 17 1023.0 10.00 17 1021.0 1.00 17 1021.0 1.00
60 4 18 1131.0 1.00 18 1119.0 1.00 18 1186.0 1.00
60 4 19 1220.0 1.00 19 1218.0 1.00 19 948.0 1.00
60 4 20 1276.0 1.00 20 1276.0 1.00 20 1270.0 1.00
60 4 21 1312.0 1.00 21 1312.0 1.00 21 1312.0 1.00
60 4 22 1330.0 0.00 22 1330.0 0.00 22 1331.0 0.10
0 4 23 1340.0 0.00 23 1340.0 0.00 23 1331.0 0.00
0 4 24 1380.0 0.00 24 1380.0 0.00 24 1380.0 0.00
60 4 25 1463.0 1.00 25 1463.0 1.00 25 1463.0 1.00
60 4 26 1463.0 0.00 26 1463.0 0.00 26 1463.0 0.00
60 4 27 1577.0 1.00 27 1576.0 1.00 27 1576.0 1.00
60 4 28 1655.0 1.00 28 1655.0 1.00 28 1645.0 1.00
0 4 29 2941.0 0.00 29 2941.0 0.00 29 2941.0 0.00
0 4 30 2941.0 0.00 30 2941.0 0.00 30 2941.0 0.00
0 4 31 2941.0 0.00 31 2941.0 0.00 31 2941.0 0.00
60 4 32 2941.0 0.00 32 2941.0 0.00 32 2941.0 0.00
60 4 33 2941.0 0.00 33 2941.0 0.00 33 2941.0 0.00
40 5 2 63.0 0.00 2 63.0 0.00 2 63.0 0.00
0 5 4 60.0 0.00 4 60.0 0.00 4 60.0 0.00
0 5 6 60.0 0.00 6 60.0 0.00 6 60.0 0.00
60 5 8 90.0 0.10 8 90.0 0.10 8 90.0 0.10
90 5 10 91.0 0.00 10 90.0 0.00 10 91.0 0.00
40 5 12 200.0 0.00 12 200.0 0.00 12 200.0 0.10
40 5 14 200.0 0.00 14 200.0 0.00 14 200.0 0.10
0 5 16 230.0 0.04 16 228.0 0.04 16 227.0 0.04
40 5 20 254.0 1.00 20 251.0 1.00 20 253.0 1.00
60 5 18 263.0 1.00 18 261.0 1.00 18 260.0 1.00
60 5 22 328.0 0.10 22 328.0 0.10 22 322.0 0.10
60 5 24 358.0 0.10 24 357.0 0.10 24 357.0 0.10
60 5 26 382.0 0.00 26 382.0 1.00 26 382.0 0.00
40 5 28 494.0 1.00 28 492.0 1.00 28 483.0 1.00
60 5 30 544.0 1.00 30 544.0 1.00 30 543.0 1.00
60 5 32 552.0 1.00 32 549.0 1.00 32 552.0 1.00
60 5 36 605.0 0.10 36 605.0 0.10 36 600.0 0.10
40 5 34 656.0 0.04 34 656.0 0.04 34 627.0 0.04
60 5 38 726.0 0.50 38 722.0 0.50 38 726.0 0.50
40 5 40 731.0 0.00 40 731.0 0.00 40 712.0 0.50
60 5 42 754.0 0.50 42 754.0 0.50 42 754.0 0.50
60 5 46 791.0 0.00 46 786.0 0.10 46 766.0 0.10
40 5 44 841.0 0.01 44 841.0 0.01 44 773.0 0.01
60 5 48 927.0 1.00 48 924.0 1.00 48 919.0 1.00
60 5 50 996.0 0.10 50 991.0 0.10 50 996.0 0.10
0 5 52 996.0 0.00 52 991.0 0.00 52 996.0 0.00
0 5 54 996.0 0.00 54 991.0 0.00 54 996.0 0.00
0 5 56 996.0 0.00 56 991.0 0.00 56 996.0 0.00
0 5 58 996.0 0.00 58 991.0 0.00 58 996.0 0.00
60 5 60 1021.0 0.50 60 1021.0 0.50 60 1015.0 0.50
60 5 62 1021.0 0.50 62 1021.0 0.50 62 1015.0 0.50
60 5 64 1133.0 1.00 64 1121.0 1.00 64 1151.0 1.00
60 5 66 1153.0 1.00 66 1145.0 1.00 66 1185.0 1.00
60 5 68 1231.0 0.10 68 1228.0 0.10 68 948.0 0.10
60 5 70 1275.0 0.10 70 1275.0 0.10 70 1267.0 0.10
60 5 72 1307.0 0.00 72 1307.0 0.00 72 1307.0 0.00
60 5 74 1323.0 0.10 74 1323.0 0.10 74 1322.0 0.10
0 5 76 1323.0 0.00 76 1323.0 0.00 76 1322.0 0.00
60 5 78 1346.0 0.00 78 1341.0 0.00 78 1342.0 0.00
0 5 80 1346.0 0.00 80 1341.0 0.00 80 1342.0 1.00
60 5 82 1378.0 1.00 82 1378.0 1.00 82 1380.0 0.00
0 5 84 1378.0 0.00 84 1378.0 0.00 84 1380.0 0.00
60 5 86 1396.0 1.00 86 1396.0 1.00 86 1392.0 1.00
60 5 88 1440.0 1.00 88 1440.0 1.00 88 1440.0 1.00
60 5 90 1456.0 1.00 90 1456.0 1.00 90 1454.0 1.00
0 5 92 1456.0 0.00 92 1456.0 0.00 92 1454.0 0.00
60 5 94 1501.0 1.00 94 1501.0 1.00 94 1494.0 1.00
0 5 96 1501.0 0.00 96 1501.0 0.00 96 1494.0 0.00
0 5 98 1501.0 0.00 98 1501.0 0.00 98 1494.0 0.00
60 5 100 1604.0 1.00 100 1604.0 1.00 100 1604.0 1.00
60 5 102 1637.0 0.00 102 1637.0 0.10 102 1620.0 0.10
60 5 112 2941.0 0.00 112 2941.0 0.00 112 2941.0 0.00
60 5 114 2941.0 0.00 114 2941.0 0.00 114 2941.0 0.00
60 5 116 2941.0 0.00 116 2941.0 0.00 116 2941.0 0.00
60 5 118 2941.0 0.00 118 2941.0 0.00 118 2941.0 0.00
60 5 124 3041.0 0.50 124 3041.0 0.50 124 2262.0 0.50
400 0 3 844.0 4.00 3 844.0 4.00 3 681.0 4.00
Nickel Octa Ethyl Porphine D4h Obs File
nipor observed freq weighted shifts no weights no order change 1/31
1=mass 2=bond 3= angle 4=dihed 5= maxbond 6=maxangle 7=maxdih
1=a1g 2=a2g 3=b1g 4=b2g 5=eg 6=a1u 7=a2u 8=b1u 9=b2u 10=eu
none Meso D N15 NI62
60 1 1 369.0 1.0 1 367.0 0.0 1 367.0 0.0 1 369.0 0.0
60 1 2 732.0 1.0 2 711.0 0.0 2 732.0 0.0 2 732.0 0.0
60 1 3 995.0 1.0 3 992.0 0.0 3 975.0 0.0 3 995.0 0.0
60 1 4 1066.0 1.0 4 1065.0 0.0 4 1065.0 0.0 4 1066.0 0.0
60 1 5 1376.0 1.0 5 1374.0 0.0 5 1374.0 0.0 5 1376.0 0.0
60 1 6 1459.0 1.0 6 1456.0 0.0 6 1459.0 0.0 6 1459.0 0.0
60 1 7 1574.0 1.0 7 1566.0 0.0 7 1574.0 0.0 7 1574.0 0.0
60 1 8 3042.0 1.0 8 2272.0 0.0 8 3042.0 0.0 8 3042.0 0.0
60 1 9 3097.0 1.0 9 3097.0 0.0 9 3097.0 0.0 9 3097.0 0.0
60 4 1 197.0 1.0 1 197.0 0.0 1 195.0 0.0 1 197.0 0.0
60 4 2 435.0 1.0 2 432.0 0.0 2 435.0 0.0 2 435.0 0.0
60 4 3 819.0 1.0 3 815.0 0.0 3 819.0 0.0 3 819.0 0.0
60 4 4 1036.0 1.0 4 1020.0 0.0 4 1017.0 0.0 4 1036.0 0.0
60 4 5 1193.0 1.0 5 1193.0 0.0 5 1193.0 0.0 5 1193.0 0.0
60 4 6 1368.0 1.0 6 1368.0 0.0 6 1368.0 0.0 6 1368.0 0.0
60 4 7 1505.0 1.0 7 1477.0 0.0 7 1499.0 0.0 7 1505.0 0.0
60 4 8 3041.0 1.0 8 2269.0 0.0 8 3041.0 0.0 8 3041.0 0.0
20 4 9 3088.0 1.0 9 3088.0 0.0 9 3088.0 0.0 9 3088.0 0.0
60 3 1 237.0 1.0 1 237.0 0.0 1 236.0 0.0 1 237.0 0.0
60 3 2 732.0 1.0 2 665.0 0.0 2 729.0 0.0 2 732.0 0.0
60 3 3 1003.0 1.0 3 1020.0 0.0 3 989.0 0.0 3 1003.0 0.0
60 3 4 1060.0 1.0 4 1066.0 0.0 4 1060.0 0.0 4 1060.0 0.0
60 3 5 1185.0 1.0 5 938.0 0.0 5 1184.0 0.0 5 1185.0 0.0
60 3 6 1319.0 1.0 6 1321.0 0.0 6 1308.0 0.0 6 1319.0 0.0
60 3 7 1505.0 1.0 7 1504.0 0.0 7 1505.0 0.0 7 1505.0 0.0
60 3 8 1650.0 1.0 8 1642.0 0.0 8 1650.0 0.0 8 1650.0 0.0
60 3 9 3097.0 1.0 9 3097.0 0.0 9 3097.0 0.0 9 3097.0 0.0
60 2 1 429.0 1.0 1 419.0 0.0 1 428.0 0.0 1 429.0 0.0
60 2 2 806.0 1.0 2 783.0 0.0 2 806.0 0.0 2 806.0 0.0
60 2 3 1005.0 1.0 3 1012.0 0.0 3 1001.0 0.0 3 1005.0 0.0
60 2 4 1139.0 1.0 4 910.0 0.0 4 1138.0 0.0 4 1139.0 0.0
60 2 5 1317.0 1.0 5 1249.0 0.0 5 1309.0 0.0 5 1317.0 0.0
60 2 6 1354.0 1.0 6 1347.0 0.0 6 1353.0 0.0 6 1354.0 0.0
60 2 7 1611.0 1.0 7 1598.0 0.0 7 1609.0 0.0 7 1611.0 0.0
60 2 9 3087.0 1.0 8 3087.0 0.0 8 3087.0 0.0 8 3087.0 0.0
60 10 2 282.0 1.0 2 280.0 0.0 2 282.0 0.0 2 277.2 0.0
60 10 4 366.0 1.0 4 349.0 0.0 4 363.0 0.0 4 366.0 0.0
60 10 6 420.0 1.0 6 411.0 0.0 6 418.0 0.0 6 417.8 0.0
60 10 8 745.0 1.0 8 648.0 0.0 8 744.0 0.0 8 745.0 0.0
60 10 10 806.0 1.0 10 807.0 0.0 10 805.0 0.0 10 806.0 0.0
60 10 12 995.0 1.0 12 999.0 0.0 12 975.0 0.0 12 995.0 0.0
60 10 14 1033.0 1.0 14 1026.0 0.0 14 1020.0 0.0 14 1033.0 0.0
60 10 16 1064.0 1.0 16 1068.0 0.0 16 1063.0 0.0 16 1064.0 0.0
60 10 18 1150.0 1.0 18 1261.0 0.0 18 1148.0 0.0 18 1150.0 0.0
60 10 20 1250.0 1.0 20 910.0 0.0 20 1248.0 0.0 20 1250.0 0.0
60 10 22 1319.0 1.0 22 1315.0 0.0 22 1309.0 0.0 22 1319.0 0.0
60 10 24 1385.0 1.0 24 1373.0 0.0 24 1373.0 0.0 24 1385.0 0.0
60 10 26 1462.0 1.0 26 1458.0 0.0 26 1457.0 0.0 26 1462.0 0.0
60 10 28 1547.0 1.0 28 1543.0 0.0 28 1546.0 0.0 28 1547.0 0.0
60 10 30 1624.0 1.0 30 1620.0 0.0 30 1623.0 0.0 30 1624.0 0.0
60 10 32 3042.0 1.0 32 2270.0 0.0 32 3042.0 0.0 32 3042.0 0.0
60 10 34 3088.0 1.0 34 3088.0 0.0 34 3088.0 0.0 34 3088.0 0.0
20 10 36 3097.0 1.0 36 3097.0 0.0 36 3097.0 0.0 36 3097.0 0.0
40 6 1 74.0 0.0 1 74.0 0.0 1 74.0 0.0 1 74.0 0.0
40 6 2 346.0 0.0 2 346.0 0.0 2 346.0 0.0 2 346.0 0.0
40 6 3 750.0 0.0 3 750.0 0.0 3 750.0 0.0 3 750.0 0.0
40 7 1 32.0 0.0 1 32.0 0.0 1 32.0 0.0 1 31.2 0.0
40 7 2 108.0 0.0 2 108.0 0.0 2 108.0 0.0 2 106.4 0.0
40 7 3 284.0 0.0 3 284.0 0.0 3 284.0 0.0 3 283.7 0.0
40 7 4 360.0 0.0 4 360.0 0.0 4 355.0 0.0 4 359.2 0.0
40 7 5 739.0 0.0 5 739.0 0.0 5 733.0 0.0 5 739.0 0.0
40 7 6 844.0 0.0 6 844.0 0.0 6 844.0 0.0 6 844.0 0.0
40 8 1 44.0 0.0 1 44.0 0.0 1 44.0 0.0 1 44.0 0.0
40 8 2 130.0 0.0 2 130.0 0.0 2 130.0 0.0 2 130.0 0.0
40 8 3 612.0 0.0 3 612.0 0.0 3 612.0 0.0 3 612.0 0.0
40 8 4 732.0 0.0 4 732.0 0.0 4 732.0 0.0 4 732.0 0.0
40 8 5 853.0 0.0 5 853.0 0.0 5 853.0 0.0 5 853.0 0.0
40 9 1 30.0 0.0 1 30.0 0.0 1 30.0 0.0 1 30.0 0.0
40 9 2 127.0 0.0 2 127.0 0.0 2 127.0 0.0 2 127.0 0.0
40 9 3 270.0 0.0 3 270.0 0.0 3 268.0 0.0 3 270.0 0.0
40 9 4 704.0 0.0 4 704.0 0.0 4 700.0 0.0 4 704.0 0.0
40 5 2 63.0 0.0 2 63.0 0.0 2 63.0 0.0 2 63.0 0.0
40 5 4 91.0 0.0 4 91.0 0.0 4 90.0 0.0 4 91.0 0.0
40 5 6 230.0 0.0 6 230.0 0.0 6 228.0 0.0 6 230.0 0.0
40 5 8 254.0 0.0 8 254.0 0.0 8 251.0 0.0 8 254.0 0.0
40 5 10 494.0 0.0 10 494.0 0.0 10 492.0 0.0 10 494.0 0.0
40 5 12 656.0 0.0 2 656.0 0.0 12 656.0 0.0 12 656.0 0.0
40 5 14 731.0 0.0 4 731.0 0.0 14 731.0 0.0 14 731.0 0.0
40 5 16 841.0 0.0 6 841.0 0.0 16 841.0 0.0 16 841.0 0.0
200 0 1 1650.0 0.0 1 1650.0 0.0 1 1650.0 0.0 1 1650.0 0.0
300 0 2 1317.0 0.0 2 1317.0 0.0 2 1250.0 0.0 2 1250.0 0.0
400 0 3 880.0 0.0 3 880.0 0.0 3 850.0 0.0 3 850.0 0.0
500 0 4 1354.0 0.0 4 1354.0 0.0 4 1350.0 0.0 4 1350.0 0.0
toluene (Cs sym) with the methyl group version 0
new file taken from ref#
3 "???" "a1 " "a2 "
none
200 0 1 1712.0 0.0
300 0 2 1530.0 0.0
400 0 3 992.0 5.0
0 1 1 220.0 1.0
0 1 2 467.0 1.0
0 1 3 522.0 1.0
0 1 4 698.0 1.0
0 1 5 732.0 1.0
0 1 6 788.0 1.0
40 1 7 898.0 1.0
40 1 8 991.0 1.0
60 1 9 1005.0 1.0
60 1 10 1030.0 1.0
60 1 11 1041.0 1.0
60 1 12 1182.0 1.0
60 1 13 1211.0 1.0
60 1 14 1380.0 1.0
60 1 15 1450.0 1.0
60 1 16 1497.0 1.0
60 1 17 1606.0 1.0
60 1 18 2900.0 1.0
60 1 19 2949.0 1.0
60 1 20 3055.0 1.0
60 1 21 3056.0 1.0
60 1 22 3057.0 1.0
0 2 1 44.0 0.2
0 2 2 348.0 1.0
0 2 3 407.0 1.0
0 2 4 622.0 1.0
0 2 5 841.0 1.0
40 2 6 967.0 1.0
40 2 7 975.0 0.5
60 2 8 1084.0 1.0
60 2 9 1157.0 1.0
60 2 10 1286.0 1.0
60 2 11 1316.0 1.0
60 2 12 1445.0 1.0
60 2 13 1468.0 1.0
60 2 14 1587.0 1.0
60 2 15 2951.0 1.0
60 2 16 3054.0 1.0
60 2 17 3055.0 1.0
#! /bin/csh
/bin/rm nmode.in
/bin/rm nmode.out
/bin/rm heme.vecs
set DIR=$AMBER1
#
cat << eof > nmode.in
Test of normal modes on heme
&data ntrun=1, cut=12.0 , drms=12.0, nvect =255, &end
eof
#
$DIR/exe/nmode -O \
-i nmode.in \
-o nmode.out \
-c min2.xyz \
-v heme.vecs || goto error
/bin/rm -f nmanal.out
cat << eof > nmanal.in
normal mode analysis, rms fluctuations
&data
ntrun = 1, nvect=255, iend=255,
pcut = 1e-3,
&end
eof
$DIR/exe/nmanal -O -i nmanal.in \
-v heme.vecs \
-o nmanal.out || goto error
exit(0)
error:
echo "Failure: run.nmode check .out and retry"
exit(1)
&symmetry
symtitle='Toluene all atoms c2v symmetry file'
thresh=0.01
iprnt=5,
nrep=13,
kgen= 4,
idgen= 9, 10, 11, 12,
termsym( 1)='???',itable(1,1 )= 9, 9, 9, 9,
termsym( 2)='A1g',itable(1,2 )= 1, 1, 1, 1,
termsym( 3)='A2g',itable(1,3 )= 1, 1,-1, 1,
termsym( 4)='A1u',itable(1,4 )= 1, 1,-1,-1,
termsym( 5)='A2u',itable(1,5 )= 1, 1, 1,-1,
termsym( 6)='B1g',itable(1,6 )= -1, 1,-1, 1,
termsym( 7)='B2g',itable(1,7 )= -1, 1, 1, 1,
termsym( 8)='B1u',itable(1,8 )= -1, 1, 1,-1,
termsym( 9)='B2u',itable(1,9 )= -1, 1,-1,-1,
termsym(10)='E1g',itable(1,10)= 1,-1, 9, 1,
termsym(11)='E1u',itable(1,11)= 1,-1, 9,-1,
termsym(12)='E2g',itable(1,12)= -1,-1, 9, 1,
termsym(13)='E2u',itable(1,13)= -1,-1, 9,-1,
numrep= 0, 2, 1, 0, 1, 0, 2, 2, 2, 2, 6, 8, 4,
nsym= 12
nasym= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12,
t_op( 1)="C6 ",
r_op(1, 1)= 0.500, 0.866, 0.000,
-0.866, 0.500, 0.000,
0.000, 0.000, 1.000,
n_op(1, 1)= 11, 12, 1, 2, 3, 4, 5, 6, 7, 8,
9, 10,
t_op( 2)="C3 ",
r_op(1, 2)= -0.500, 0.866, 0.000,
-0.866, -0.500, 0.000,
0.000, 0.000, 1.000,
n_op(1, 2)= 9, 10, 11, 12, 1, 2, 3, 4, 5, 6,
7, 8,
t_op( 3)="sxz",
r_op(1, 3)= 1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 3)= 9, 10, 7, 8, 5, 6, 3, 4, 1, 2,
11, 12,
t_op( 4)="i ",
r_op(1, 4)= -1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, -1.000,
n_op(1, 4)= 7, 8, 9, 10, 11, 12, 1, 2, 3, 4,
5, 6,
&end
&symmetry
symtitle='Toluene all atoms c2v symmetry file'
thresh=0.01,
iprnt=0,
nrep=3,
kgen= 0,
termsym( 1)='???',itable(1,1 )= 9, 9, 9, 9,
termsym( 2)='A1 ',itable(1,2 )= 1, 1, 1, 1,
termsym( 3)='A2 ',itable(1,3 )= 1,-1, 1,-1,
numrep= 0, 27, 21,
nsym= 18,
thresh= 0.01,
nasym= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18,
t_op( 1)="E ",
r_op(1, 1)= 1.000, 0.000, 0.000,
0.000, 1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 1)= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18,
t_op( 2)="sxz",
r_op(1, 2)= 1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 2)= 9, 10, 7, 8, 5, 6, 3, 4, 1, 2,
11, 12, 13, 15, 14, 16, 18, 17,
t_op( 3)="E ",
r_op(1, 3)= 1.000, 0.000, 0.000,
0.000, 1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 3)= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18,
t_op( 4)="sxz",
r_op(1, 4)= 1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 4)= 9, 10, 7, 8, 5, 6, 3, 4, 1, 2,
11, 12, 13, 15, 14, 16, 18, 17,
&end
Nickel Octa Ethyl Porphine Symmetry File
&symmetry
symtitle='Nioepy all atom d2d symmetry file'
thresh= 9.9999998E-03
nsym=85,
iprnt=1,
nrep=6,
termsym(1)='???',itable(1,1)= 9, 9, 9, 9
termsym(2)='A1 ',itable(1,2)= 1, 1, 1, 9
termsym(3)='A2 ',itable(1,3)= 1,-1, 1, 9
termsym(4)='B1 ',itable(1,4)= -1, 1, 1, 9
termsym(5)='B2 ',itable(1,5)= -1,-1, 1, 9
termsym(6)='E ',itable(1,6)= 9, 9, 1,-1
numrep=0,31, 31, 30, 33, 124,
nsym= 85
nasym= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30,
31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
61, 62, 63, 64, 65, 66, 67, 68, 69, 70,
71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
81, 82, 83, 84, 85,
t_op( 1)="S14",
r_op(1, 1)= 0.000, -1.000, 0.000,
1.000, 0.000, 0.000,
0.000, 0.000, -1.000,
n_op(1, 1)= 1, 23, 24, 25, 26, 27, 28, 29, 30, 32,
31, 33, 34, 35, 36, 37, 38, 40, 39, 41,
42, 43, 44, 45, 46, 47, 48, 49, 50, 51,
53, 52, 54, 55, 56, 57, 58, 59, 61, 60,
62, 63, 64, 65, 66, 67, 68, 69, 70, 71,
72, 74, 73, 75, 76, 77, 78, 79, 80, 82,
81, 83, 84, 85, 2, 3, 4, 5, 6, 7,
8, 9, 11, 10, 12, 13, 14, 15, 16, 17,
19, 18, 20, 21, 22,
t_op( 2)="C_2",
r_op(1, 2)= 0.000, 1.000, 0.000,
1.000, 0.000, 0.000,
0.000, 0.000, -1.000,
n_op(1, 2)= 1, 23, 41, 33, 34, 36, 35, 37, 38, 39,
40, 25, 26, 28, 27, 29, 30, 31, 32, 24,
21, 22, 2, 20, 12, 13, 15, 14, 16, 17,
18, 19, 4, 5, 7, 6, 8, 9, 10, 11,
3, 84, 85, 65, 83, 75, 76, 78, 77, 79,
80, 81, 82, 67, 68, 70, 69, 71, 72, 73,
74, 66, 63, 64, 44, 62, 54, 55, 57, 56,
58, 59, 60, 61, 46, 47, 49, 48, 50, 51,
52, 53, 45, 42, 43,
t_op( 3)=" E",
r_op(1, 3)= 1.000, 0.000, 0.000,
0.000, 1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 3)= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30,
31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
51, 52, 53, 54, 55, 56, 57, 58, 59, 60,
61, 62, 63, 64, 65, 66, 67, 68, 69, 70,
71, 72, 73, 74, 75, 76, 77, 78, 79, 80,
81, 82, 83, 84, 85,
t_op( 4)="C2p",
r_op(1, 4)= -1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 4)= 1, 44, 45, 46, 47, 48, 49, 50, 51, 52,
53, 54, 55, 56, 57, 58, 59, 60, 61, 62,
63, 64, 65, 66, 67, 68, 69, 70, 71, 72,
73, 74, 75, 76, 77, 78, 79, 80, 81, 82,
83, 84, 85, 2, 3, 4, 5, 6, 7, 8,
9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
29, 30, 31, 32, 33, 34, 35, 36, 37, 38,
39, 40, 41, 42, 43,
&end
Nickel Octa Ethyl Porphine D4h Symmetry File
&symmetry
thresh=0.01,
nsym=37,
iprnt=1,
nrep=11,
termsym(1)='???',itable(1,1)= 9, 9, 9, 9,
termsym(2)='A1g',itable(1,2)= 1, 1, 1, 9
termsym(3)='A2g',itable(1,3)= 1,-1, 1, 9
termsym(4)='B1g',itable(1,4)= -1, 1, 1, 9
termsym(5)='B2g',itable(1,5)= -1, 9, 1, 9
termsym(6)='E g',itable(1,6)= 0, 9, 1,-1
termsym(7)='A1u',itable(1,7)= 1, 1,-1, 9
termsym(8)='A2u',itable(1,8)= 1,-1,-1, 9
termsym(9)='B1u',itable(1,9)= -1, 1,-1, 9
termsym(10)='B2u',itable(1,10)= -1,-1,-1, 9
termsym(11)='E u',itable(1,11)= 0, 9,-1,-1
numrep=0,9,8,9,9,16,3,6,5,4,36
nsym= 37
nasym= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30,
31, 32, 33, 34, 35, 36, 37,
t_op( 1)="C14",
r_op(1, 1)= 0.000, 1.000, 0.000,
-1.000, 0.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 1)= 1, 29, 30, 31, 32, 33, 34, 35, 36, 37,
2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
12, 13, 14, 15, 16, 17, 18, 19, 20, 21,
22, 23, 24, 25, 26, 27, 28,
t_op( 2)="C2p",
r_op(1, 2)= 1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, -1.000,
n_op(1, 2)= 1, 2, 8, 6, 7, 4, 5, 3, 36, 37,
29, 35, 33, 34, 31, 32, 30, 27, 28, 20,
26, 24, 25, 22, 23, 21, 18, 19, 11, 17,
15, 16, 13, 14, 12, 9, 10,
t_op( 3)=" i",
r_op(1, 3)= -1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, -1.000,
n_op(1, 3)= 1, 20, 21, 22, 23, 24, 25, 26, 27, 28,
29, 30, 31, 32, 33, 34, 35, 36, 37, 2,
3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19,
t_op( 4)="C2n",
r_op(1, 4)= -1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 4)= 1, 20, 21, 22, 23, 24, 25, 26, 27, 28,
29, 30, 31, 32, 33, 34, 35, 36, 37, 2,
3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18, 19,
&end
&symmetry
symtitle='Toluene all atoms c2v symmetry file'
thresh=0.01,
iprnt=0,
nrep=3,
kgen= 0,
termsym( 1)='???',itable(1,1 )= 9, 9, 9, 9,
termsym( 2)='A1 ',itable(1,2 )= 1, 1, 1, 1,
termsym( 2)='A2 ',itable(1,3 )= 1,-1, 1,-1,
numrep= 0, 22, 17,
nsym= 15,
thresh= 0.01,
nasym= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15,
t_op( 1)="E ",
r_op(1, 1)= 1.000, 0.000, 0.000,
0.000, 1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 1)= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15,
t_op( 2)="sxz",
r_op(1, 2)= 1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 2)= 9, 10, 7, 8, 5, 6, 3, 4, 1, 2,
11, 12, 13, 15, 14,
t_op( 3)="E ",
r_op(1, 3)= 1.000, 0.000, 0.000,
0.000, 1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 3)= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15,
t_op( 4)="sxz",
r_op(1, 4)= 1.000, 0.000, 0.000,
0.000, -1.000, 0.000,
0.000, 0.000, 1.000,
n_op(1, 4)= 9, 10, 7, 8, 5, 6, 3, 4, 1, 2,
11, 12, 13, 15, 14,
&end
ethylbenzene in entirety
BOND
CA-CA 427.010 1.400
CA-HA 366.200 1.080
ANGLE
CA-CA-CA 71.673 120.000
CA-CA-HA 36.178 120.000
DIHEDRAL
CA-CA-CA-CA 1 4.178 180.000 2.000
CA-CA-CA-HA 2 8.063 180.000 2.000
HA-CA-CA-HA 1 2.292 180.000 2.000
IMPROPER
CA-CA-HA-CA 1 0.000 180.000 2.000
CA-HA-CA-CA 1 0.000 180.000 2.000
ethylbenzene in entirety
MASS
HM 1.008
HA 1.008
CC 12.001
BOND
CA-CA 414.908 1.400
CA-HA 366.200 1.080
CA-CC 358.353 1.400
CT-CT 337.148 1.526
CT-HC 325.634 1.090
CC-CT 313.846 1.510
CT-HM 337.442 1.090
ANGLE
CA-CA-CA 77.041 120.000
CA-CA-HA 35.348 120.000
CC-CA-HA 35.348 120.000
CC-CT-HC 50.290 109.500
CA-CC-CA 68.932 120.000
CA-CA-CC 78.335 120.000
CA-CC-CT 42.863 120.000
HM-CT-CT 49.415 109.500
HC-CT-CT 47.204 109.500
CC-CT-CT 58.916 109.500
HM-CT-HM 31.286 109.500
HC-CT-HC 31.286 109.500
DIHEDRAL
CA-CA-CA-CA 1 3.407 180.000 2.000
CA-CA-CA-HA 2 8.330 180.000 2.000
HA-CA-CA-HA 1 2.335 180.000 2.000
CA-CA-CC-CT 1 3.475 180.000 2.000
CA-CA-CC-CA 1 4.626 180.000 2.000
HA-CA-CC-CT 1 2.100 180.000 2.000
HA-CA-CC-CA 1 4.009 180.000 2.000
CA-CC-CT-HC 4 0.600 180.000 3.000
HM-CT-CT-HC 6 1.254 0.000 3.000
HM-CT-CT-CC 3 0.000 0.000 3.000
CA-CC-CT-CT 2 0.560 180.000 -4.000
CA-CC-CT-CT 2 0.000 180.000 -3.000
CA-CC-CT-CT 2 2.308 180.000 2.000
IMPROPER
CA-CC-CT-CA 1 4.143 180.000 2.000
CA-CT-CC-CA 1 4.143 180.000 2.000
X -HA-CA-X 1 0.000 180.000 2.000
X -CA-HA-X 1 0.000 180.000 2.000
HBOND
HW OW 225. 0000. 4.
NONBON
HM 1.54 0.01 0.00000
HA 1.54 0.01 0.00000
Jason aveaged rest5.final
HP beta hydrogen
HM meso hydrogen
w running a simplex routine with run.simple5 on correct sym
CX beta c1 of ethane
CY beta c2 of ethane 15.03 amu
added imidazole atom types
corrected LC-LO force constant
united methyl atom (CX)
MASS
HM 1.008
HI 1.008
HE 1.008
HN 1.008
HQ 1.008
NO 14.01
NP 14.01
CX 12.01
CY 12.01
CQ 12.01
CD 12.01
LC 12.01
LO 16.01
BOND
FE-NP 110.308 1.930
FE-NO 110.308 1.930
NP-CC 335.936 1.380
NO-CC 335.936 1.380
CC-CB 330.655 1.440
CC-CD 365.547 1.380
CB-CB 460.380 1.350
CD-HM 363.015 1.090
CB-CX 316.227 1.501
CX-CY 310.552 1.506
CX-HE 337.442 1.100
CY-HN 337.442 1.100
CB-CQ 316.277 1.500
CQ-CQ 549.000 1.313
CQ-HQ 340.000 1.090
CV-HC 367.000 1.090
CR-HC 367.000 1.090
CY-C 317.000 1.090
LC-LO 1075.000 1.200
FE-LC 140.000 2.110
FE-NB 110.308 1.930
ANGLE
NP-FE-NP 0.000 180.000
NO-FE-NO 0.000 180.000
NO-FE-NP 9.981 90.000
FE-NP-CC 80.289 120.000
FE-NO-CC 80.289 120.000
CB-CB-CX 26.414 120.000
CC-CB-CX 26.414 120.000
CB-CX-HE 39.778 109.500
CY-CX-HE 53.997 109.500
CB-CX-CY 65.618 109.500
CB-CC-CD 49.662 120.000
CC-NP-CC 62.010 120.000
CC-NO-CC 62.010 120.000
CC-CB-CB 72.582 120.000
CC-CD-CC 92.601 120.000
NO-CC-CD 43.773 120.000
NP-CC-CD 43.773 120.000
NO-CC-CB 101.511 120.000
NP-CC-CB 101.511 120.000
HN-CY-CX 43.457 109.500
CC-CD-HM 31.413 120.000
HE-CX-HE 32.614 109.500
HN-CY-HN 32.614 109.500
CQ-CB-CC 70.000 120.000
CQ-CB-CB 70.000 120.000
CQ-CQ-CB 70.000 120.000
HQ-CQ-CB 35.000 120.000
HQ-CQ-CQ 35.000 120.000
HQ-CQ-HQ 35.000 120.000
NB-FE-NO 50.000 90.000
NB-FE-NP 50.000 90.000
NB-FE-LC 0.000 180.000
CV-NB-FE 0.000 110.000
CR-NB-FE 0.000 110.000
FE-LC-LO 65.000 180.000
NP-FE-LC 45.000 90.000
NO-FE-LC 45.000 90.000
HC-CY-C 50.000 109.500
CX-CY-C 63.000 110.100
CY-C -O2 70.000 117.000
N -CT-HC 50.000 109.500
CC-CV-HC 50.000 120.000
NA-CR-HC 35.000 109.500
HC-CR-NB 35.000 109.500
NB-CV-HC 50.000 120.000
HN-CY-C 50.000 109.500
DIHEDRAL
CC-NO-FE-NP 4 7.122 180.000 2.000
CC-NO-FE-NO 2 0.000 180.000 2.000
CC-NO-FE-NB 2 0.000 180.000 2.000
CC-NO-FE-LC 2 0.000 180.000 2.000
CC-NP-FE-NO 4 7.222 180.000 2.000
CC-NP-FE-NP 2 0.000 180.000 2.000
CC-NP-FE-NB 2 0.000 180.000 2.000
CC-NP-FE-LC 2 0.000 180.000 2.000
X -NB-FE-X 8 0.000 180.000 2.000
X -FE-NB-X 8 0.000 180.000 2.000
CB-CB-CX-CY 1 0.280 180.000 -4.000
CB-CB-CX-CY 1 0.000 180.000 -3.000
CB-CB-CX-CY 1 1.154 180.000 2.000
CC-CB-CX-CY 1 0.280 180.000 -4.000
CC-CB-CX-CY 1 0.000 180.000 -3.000
CC-CB-CX-CY 1 1.154 180.000 2.000
CB-CB-CX-HE 2 0.300 180.000 2.000
CC-CB-CX-HE 2 0.300 180.000 2.000
HE-CX-CY-HN 6 1.254 0.000 3.000
CB-CX-CY-HN 3 0.000 0.000 3.000
CC-CB-CB-CC 1 7.759 180.000 2.000
CX-CB-CB-CX 1 5.579 180.000 2.000
CC-CB-CB-CX 2 3.475 180.000 2.000
NO-CC-CB-CX 1 2.811 180.000 2.000
NP-CC-CB-CX 1 2.811 180.000 2.000
FE-NO-CC-CB 1 3.113 180.000 2.000
FE-NP-CC-CB 1 3.113 180.000 2.000
FE-NP-CC-CD 1 3.701 180.000 2.000
FE-NO-CC-CD 1 3.701 180.000 2.000
FE-CC-CB-CB 1 0.193 180.000 2.000
NP-CC-CB-CB 1 0.193 180.000 2.000
CC-NO-CC-CD 1 2.390 180.000 2.000
CC-NP-CC-CD 1 2.390 180.000 2.000
CD-CC-CB-CX 1 1.398 180.000 2.000
CD-CC-CB-CB 1 6.699 180.000 2.000
CC-NO-CC-CB 1 4.244 180.000 2.000
CC-NP-CC-CB 1 4.244 180.000 2.000
CC-CD-CC-NO 1 3.685 180.000 2.000
CC-CD-CC-NP 1 3.685 180.000 2.000
HM-CD-CC-CB 1 1.878 180.000 2.000
CC-CD-CC-CB 1 1.106 180.000 2.000
HM-CD-CC-NO 1 2.616 180.000 2.000
HM-CD-CC-NP 1 2.616 180.000 2.000
NO-CC-CB-CQ 1 6.547 180.000 2.000
NP-CC-CB-CQ 1 6.547 180.000 2.000
NO-CC-CB-CB 1 6.547 180.000 2.000
NP-CC-CB-CB 1 6.547 180.000 2.000
HQ-CQ-CB-CB 1 0.823 180.000 2.000
HQ-CQ-CB-CC 1 0.823 180.000 2.000
CQ-CQ-CB-CC 2 1.933 180.000 2.000
CQ-CQ-CB-CB 2 1.933 180.000 2.000
HQ-CQ-CQ-HQ 2 14.659 180.000 2.000
CC-CQ-CQ-HQ 1 10.512 180.000 2.000
CB-CQ-CQ-HQ 1 10.512 180.000 2.000
CQ-CB-CC-CD 1 1.398 180.000 2.000
X -FE-LC-X 4 0.000 180.000 2.000
X -CX-CY-X 9 1.400 0.000 3.000
X -C -CY-X 4 0.000 0.000 2.000
IMPROPER
X -CD-HM-X 0 0.000 180.000 2.000
X -CB-CX-X 0 4.314 180.000 2.000
CC-NO-FE-CC 0 3.600 180.000 2.000
CC-NP-FE-CC 0 3.600 180.000 2.000
CC-NO-CD-CB 0 1.108 180.000 2.000
CC-NP-CD-CB 0 1.108 180.000 2.000
X -CC-CC-X 0 0.000 180.000 2.000
X -CC-CB-X 0 0.000 180.000 2.000
X -CB-CC-X 0 0.000 180.000 2.000
X -NP-CB-X 0 0.000 180.000 2.000
X -NO-CB-X 0 0.000 180.000 2.000
X -CB-NO-X 0 0.000 180.000 2.000
X -CB-NP-X 0 0.000 180.000 2.000
X -CB-CQ-X 0 4.314 180.000 2.000
HBOND
HW OW 225. 0000. 4.
NONBON
HW 1.00 0.020 0.0
CL 2.223 0.107 0.0
FE 1.20000 0.05000 0.00000
LO 1.60000 0.20000 0.00000
LC 1.85 0.12 0.00000
HM 1.54 0.01 0.00000
HP 1.54 0.01 0.00000
HE 1.54 0.01 0.00000
HI 1.54 0.01 0.00000
HN 1.54 0.01 0.00000
HQ 1.54 0.01 0.00000
CX 1.9080 0.1094 0.000
CY 1.80 0.06 0.00000
C9 1.80 0.06 0.000
C8 1.80 0.06 0.0000
CQ 1.80 0.06 0.0000
Heme Sundar New Potential File
Jason aveaged rest5.final
HP beta hydrogen
HM meso hydrogen
w running a simplex routine with run.simple5 on correct sym
CX beta c1 of ethane
CY beta c2 of ethane 15.03 amu
added imidazole atom types
corrected LC-LO force constant
united methyl atom (CX)
MASS
HM 1.008
HI 1.008
HE 1.008
HN 1.008
NI 58.69
NO 14.01
NP 14.01
CX 12.01
CY 12.01
CD 12.01
BOND
NI-NP 80.308 1.860
NI-NO 80.308 1.860
NP-CC 335.936 1.380
NO-CC 335.936 1.380
CC-CB 330.655 1.440
CC-CD 365.547 1.380
CB-CB 460.380 1.350
CD-HM 363.015 1.090
CB-CX 316.227 1.495
CX-CY 310.552 1.506
CX-HE 337.462 1.100
CY-HN 337.462 1.100
ANGLE
NP-NI-NP 0.000 180.000
NO-NI-NO 0.000 180.000
NO-NI-NP 9.981 90.000
NI-NP-CC 80.289 120.000
NI-NO-CC 80.289 120.000
CB-CB-CX 26.414 120.000
CC-CB-CX 26.414 120.000
CB-CX-HE 39.778 109.500
CY-CX-HE 53.997 109.500
CB-CX-CY 65.618 109.500
CB-CC-CD 49.662 120.000
CC-NP-CC 62.010 120.000
CC-NO-CC 62.010 120.000
CC-CB-CB 72.582 120.000
CC-CD-CC 92.601 120.000
NO-CC-CD 43.773 120.000
NP-CC-CD 43.773 120.000
NO-CC-CB 101.511 120.000
NP-CC-CB 101.511 120.000
HN-CY-CX 43.457 109.500
CC-CD-HM 31.413 120.000
HE-CX-HE 32.614 109.500
HN-CY-HN 32.614 109.500
DIHEDRAL
CC-NO-NI-NP 4 7.122 180.000 2.000
CC-NO-NI-NO 2 0.000 180.000 2.000
CC-NP-NI-NO 4 7.122 180.000 2.000
CC-NP-NI-NP 2 0.000 180.000 2.000
CB-CB-CX-CY 1 0.280 180.000 -4.000
CB-CB-CX-CY 1 0.000 180.000 -3.000
CB-CB-CX-CY 1 1.154 180.000 2.000
CC-CB-CX-CY 1 0.280 180.000 -4.000
CC-CB-CX-CY 1 0.000 180.000 -3.000
CC-CB-CX-CY 1 1.154 180.000 2.000
CB-CB-CX-HE 2 0.300 180.000 2.000
CC-CB-CX-HE 2 0.300 180.000 2.000
HE-CX-CY-HN 6 1.254 0.000 3.000
CB-CX-CY-HN 3 0.000 0.000 3.000
CC-CB-CB-CC 1 7.579 180.000 2.000
CX-CB-CB-CX 1 5.579 180.000 2.000
CC-CB-CB-CX 2 3.475 180.000 2.000
NO-CC-CB-CX 1 2.811 180.000 2.000
NP-CC-CB-CX 1 2.811 180.000 2.000
NI-NO-CC-CB 1 3.113 180.000 2.000
NI-NP-CC-CB 1 3.113 180.000 2.000
NI-NP-CC-CD 1 3.701 180.000 2.000
NI-NO-CC-CD 1 3.701 180.000 2.000
NO-CC-CB-CB 1 0.193 180.000 2.000
NP-CC-CB-CB 1 0.193 180.000 2.000
CC-NO-CC-CD 1 2.390 180.000 2.000
CC-NP-CC-CD 1 2.390 180.000 2.000
CD-CC-CB-CX 1 1.398 180.000 2.000
CD-CC-CB-CB 1 6.699 180.000 2.000
CC-NO-CC-CB 1 4.244 180.000 2.000
CC-NP-CC-CB 1 4.244 180.000 2.000
CC-CD-CC-NO 1 3.685 180.000 2.000
CC-CD-CC-NP 1 3.685 180.000 2.000
HM-CD-CC-CB 1 1.878 180.000 2.000
CC-CD-CC-CB 1 1.106 180.000 2.000
HM-CD-CC-NO 1 2.616 180.000 2.000
HM-CD-CC-NP 1 2.616 180.000 2.000
IMPROPER
X -CD-HM-X 0 0.000 180.000 2.000
X -CB-CX-X 0 4.314 180.000 2.000
CC-NO-NI-CC 0 3.600 180.000 2.000
CC-NP-NI-CC 0 3.600 180.000 2.000
CC-NO-CD-CB 0 1.108 180.000 2.000
CC-NP-CD-CB 0 1.108 180.000 2.000
HBOND
HW OW 225. 0000. 4.
NONBON
HW 1.00 0.020 0.0
CL 2.223 0.107 0.0
NI 1.20000 0.05000 0.00000
LO 1.60000 0.20000 0.00000
LC 1.85 0.12 0.00000
HM 1.54 0.01 0.00000
HP 1.54 0.01 0.00000
HE 1.54 0.01 0.00000
HI 1.54 0.01 0.00000
HN 1.54 0.01 0.00000
CX 1.9080 0.1094 0.000
CY 1.80 0.06 0.00000
C9 1.80 0.06 0.000
C8 1.80 0.06 0.0000
Heme Sundar Old Potential File
Jason aveaged rest5.final
HP beta hydrogen
HM meso hydrogen
w running a simplex routine with run.simple5 on correct sym
CX beta c1 of ethane
CY beta c2 of ethane 15.03 amu
added imidazole atom types
corrected LC-LO force constant
united methyl atom (CX)
MASS
HM 1.008
HI 1.008
HE 1.008
HN 1.008
NI 58.69
NO 14.01
NP 14.01
CX 12.01
CY 12.01
CD 12.01
BOND
NI-NP 157.246 1.958
NI-NO 157.246 1.958
NP-CC 297.322 1.376
NO-CC 297.322 1.376
CC-CB 260.679 1.443
CC-CD 327.507 1.371
CB-CB 413.606 1.346
CD-HM 356.593 1.090
CB-CX 282.851 1.501
CX-CY 329.418 1.506
CX-HE 337.442 1.100
CY-HN 337.442 1.100
ANGLE
NP-NI-NP 0.000 180.000
NO-NI-NO 0.000 180.000
NO-NI-NP 8.780 90.000
NI-NP-CC 87.705 120.000
NI-NO-CC 87.705 120.000
NO-CC-CB 117.615 120.000
NP-CC-CB 117.615 120.000
NO-CC-CD 36.191 121.800
NP-CC-CD 36.191 121.800
CB-CC-CD 36.117 118.200
CC-NP-CC 130.413 108.000
CC-NO-CC 130.413 108.000
CC-CB-CB 90.796 120.000
CC-CD-CC 166.070 124.000
CB-CX-HE 55.062 109.500
CB-CX-CY 93.004 109.500
CB-CB-CX 29.230 120.000
CC-CB-CX 29.230 120.000
CY-CX-HE 35.847 109.500
HN-CY-CX 35.847 109.500
CC-CD-HM 32.014 119.300
HE-CX-HE 31.560 109.500
HN-CY-HN 31.560 109.500
DIHEDRAL
CC-NO-NI-NP 4 7.122 180.000 2.000
CC-NO-NI-NO 2 0.000 180.000 2.000
CC-NP-NI-NO 4 7.122 180.000 2.000
CC-NP-NI-NP 2 0.000 180.000 2.000
CB-CB-CX-CY 1 0.280 180.000 -4.000
CB-CB-CX-CY 1 0.000 180.000 -3.000
CB-CB-CX-CY 1 1.154 180.000 2.000
CC-CB-CX-CY 1 0.280 180.000 -4.000
CC-CB-CX-CY 1 0.000 180.000 -3.000
CC-CB-CX-CY 1 1.154 180.000 2.000
CB-CB-CX-HE 2 0.300 180.000 2.000
CC-CB-CX-HE 2 0.300 180.000 2.000
HE-CX-CY-HN 6 1.254 0.000 3.000
CB-CX-CY-HN 3 0.000 0.000 3.000
CC-CB-CB-CC 1 7.579 180.000 2.000
CX-CB-CB-CX 1 5.579 180.000 2.000
CC-CB-CB-CX 2 3.475 180.000 2.000
NO-CC-CB-CX 1 2.811 180.000 2.000
NP-CC-CB-CX 1 2.811 180.000 2.000
NI-NO-CC-CB 1 3.113 180.000 2.000
NI-NP-CC-CB 1 3.113 180.000 2.000
NI-NP-CC-CD 1 3.701 180.000 2.000
NI-NO-CC-CD 1 3.701 180.000 2.000
NO-CC-CB-CB 1 0.193 180.000 2.000
NP-CC-CB-CB 1 0.193 180.000 2.000
CC-NO-CC-CD 1 2.390 180.000 2.000
CC-NP-CC-CD 1 2.390 180.000 2.000
CD-CC-CB-CX 1 1.398 180.000 2.000
CD-CC-CB-CB 1 6.699 180.000 2.000
CC-NO-CC-CB 1 4.244 180.000 2.000
CC-NP-CC-CB 1 4.244 180.000 2.000
CC-CD-CC-NO 1 3.685 180.000 2.000
CC-CD-CC-NP 1 3.685 180.000 2.000
HM-CD-CC-CB 1 1.878 180.000 2.000
CC-CD-CC-CB 1 1.106 180.000 2.000
HM-CD-CC-NO 1 2.616 180.000 2.000
HM-CD-CC-NP 1 2.616 180.000 2.000
IMPROPER
X -CD-HM-X 0 0.000 180.000 2.000
X -CB-CX-X 0 2.314 180.000 2.000
CC-NO-NI-CC 0 3.600 180.000 2.000
CC-NP-NI-CC 0 3.600 180.000 2.000
CC-NO-CD-CB 0 1.108 180.000 2.000
CC-NP-CD-CB 0 1.108 180.000 2.000
HBOND
HW OW 225. 0000. 4.
NONBON
HW 1.00 0.020 0.0
CL 2.223 0.107 0.0
NI 1.20000 0.05000 0.00000
LO 1.60000 0.20000 0.00000
LC 1.85 0.12 0.00000
HM 1.54 0.01 0.00000
HP 1.54 0.01 0.00000
HE 1.54 0.01 0.00000
HI 1.54 0.01 0.00000
HN 1.54 0.01 0.00000
CX 1.9080 0.1094 0.000
CY 1.80 0.06 0.00000
C9 1.80 0.06 0.000
C8 1.80 0.06 0.0000
Toluene with all same HC
MASS
HC 1.008
HA 1.008
CC 12.001
BOND
CA-CA 414.547 1.400
CA-HA 366.200 1.080
CT-HC 325.634 1.090
CA-CC 357.966 1.400
CC-CT 315.148 1.510
ANGLE
CA-CA-HA 35.348 120.000
CA-CA-CA 74.538 120.000
CC-CT-HC 50.290 109.500
HC-CT-HC 31.869 109.500
CC-CA-HA 31.041 120.000
CA-CC-CA 69.231 120.000
CA-CA-CC 78.657 120.000
CA-CC-CT 51.857 120.000
DIHEDRAL
CA-CA-CA-CA 1 3.407 180.000 2.000
CA-CA-CA-HA 2 8.330 180.000 2.000
HA-CA-CA-HA 1 2.335 180.000 2.000
CA-CA-CC-CT 1 3.475 180.000 2.000
CA-CA-CC-CA 1 4.626 180.000 2.000
HA-CA-CC-CT 1 2.100 180.000 2.000
HA-CA-CC-CA 1 4.009 180.000 2.000
CA-CC-CT-HC 6 0.900 180.000 3.000
IMPROPER
X -CA-HA-X 1 0.000 180.000 2.000
X -HA-CA-X 1 0.000 180.000 2.000
CA-CC-CT-CA 1 2.764 180.000 2.000
CA-CT-CC-CA 1 2.764 180.000 2.000
HBOND
HW OW 225. 0000. 4.
NONBON
HC 1.54 0.01 0.00000
HA 1.54 0.01 0.00000