depends on the stiffness of the chemical bond as determined by its force constant
k and on the mass of the atoms as determined by the reduced mass 
.
Normal Modes of Vibration
This page will run with Microsoft explorer and the CHIME SP6
plugin.
A version with more features can be run with Netscape version
There are many different forms of radiant energy for example: ultraviolet, visible, and infrared light. All light is essentially the same, it consists of an oscillating electromagnetic field, but we perceive it in different forms depending on its wavelength or frequency. Infrared radiation has relatively long wavelengths (2 microns) and frequencies (2000 cm-1). The cm-1 is a special unit of frequency called the wavenumber which is just one over the wavelength in cm. Multiplying the frequency in wavenumbers by the speed of light ( 3x10^10 cm/sec ) will give the frequency sec-1. Infrared light is oscillating very quickly over ten thousand billion times a second (6x10^13).
We will be concerned primarily with the middle infrared region with frequencies from about 300 cm-1 to 3000 cm-1. It is the type of radiation that is given off by embers in a fire and which you sense as warmth. On a microscopic scale molecular vibrations have the same frequency as infrared radiation. For this reason Infrared radiation is absorbed primarily by molecular vibrations. Molecules also rotate but the rotational motion is slow compared to the vibration. Microwave radiation 0.1 cm-1 to 20 cm-1 is absorbed by the rotation of molecules. In an infrared spectrum molecular vibrations determine the position of the peaks while the rotational motion broadens and adds fine structure to the peaks.
The measurement of the amount of light absorbed as a function of the wavenumber or frequency generates a spectrum. The infrared spectrum of a molecule is a useful chemical tool. In organic chemistry it can be used to determine the types of functional groups in a molecule. In analytical chemistry the intensity of the peaks provide a analytical measure of the amount of substance present. Finally in physical chemistry the position of the peaks gives information about the vibrational frequencies and the intensity of the peaks gives information about the symmetry of the vibrations. All of this information is extremely useful in characterizing molecules. To analyze an infrared spectrum we need to understand how the position and intensity of the peaks is related to the vibrations of the molecule.
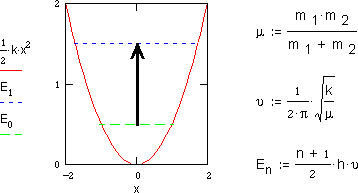
As the picture at the top of this page shows, atoms in a molecule do not maintain
fixed positions but actually vibrate back and forth about an average bond distances.
Since this motion is microscopic it is quantitized into discrete energy states
by the laws of quantum mechanics. These laws indicate that for the simple stretching
motion of a diatomic molecule the vibrational frequency
depends on the stiffness of the chemical bond as determined by its force constant
k and on the mass of the atoms as determined by the reduced mass .
Stiff double bonds with large force constants vibrate faster than loose single bonds and heavy atoms will vibrate slower than light atoms. For this reason organic functional groups that have characteristic masses and bond strengths fall into particular regions in the infrared spectrum. For example, the light hydrogen atom in a carbon hydrogen bond stretches at large frequencies of about 3000 cm-1. Stretching frequencies in inorganic complexes on the other hand occur at low frequencies because the atoms are heavy and weakly bonded. For example, Mo-Cl bond stretching occurs in the far infrared at about 250 cm-1. Finally, bond bending force constants are much smaller than stretching force constants so even carbon hydrogen bending modes occur at lower frequencies around 1200 cm-1.
The energy of a vibrating molecule En is given by a vibrational
quantum number n, Planck's constant h, and the fundamental vibration frequency
. h is the fundamental quantum of energy
and equals the energy spacing between each energy level. At room temperature
most of the molecules will be in their lowest vibrational energy state or zero-point
energy E0. This is the stable vibrating state of a molecule. Here
the molecules will remain until they receive a quantum of energy.
Absorption of light with the appropriate energy ( h =
E1-E0 ) allows the molecule to become "excited" into the
next higher vibrational energy state E1. Such absorption of infrared
light can only occur, if the dipole moment of the molecule is different in the
two vibrational states. This changing dipole results in a molecular oscillating
electric field. Since light itself is a oscillating electric field it can use
the oscillating molecular dipole as a electronic handle to grab and shake the
molecule into a higher vibrational state. The requirement that the absorption
of a vibrational quantum be accompanied by a change in dipole moment is an example
of a spectroscopic selection rule. Vibrational transitions that obey this rule
are said to be infrared active and will intensely absorb light. Vibrational
transitions that do not change the dipole are said to infrared-inactive and
result in very weak absorption bands. For example, carbon monoxide and hydrogen
chloride, which have permanent dipoles, absorb infrared light, but diatomic
hydrogen or oxygen without dipoles do not. Further more, in a symmetric polyatomic
molecule like carbon dioxide only the asymmetric vibrations that create a dipole
will be infrared-active.Would water (H2O) absorb strongly
in the infrared?(1)
Complex polyatomic molecules like carbon dioxide have more possible vibrations. Each fundamental type of vibation of a polyatomic molecule is called a normal mode. A normal mode is a collective motion of all the atoms in the molecule where each atom in the molecule moves in phase with each other at a particular frequency. A nonlinear molecule,like methylene dichloride (CH2Cl2), containing N atoms can have 3N-6 fundamental or normal modes of vibration, while a linear molecule like carbon dioxide can have 3N-5 normal modes of vibration. As a result, the infrared spectrum of organic molecules are rather complex. Methylene dichloride with 5 atoms would have 9 different normal modes of vibration. How many vibrations would carbon dioxide (CO2) have?(2)
The complex spectrum of a Polyatomic organic compound has two distinct classes of molecular vibrations, stretching and bending. Stretching vibrations change the bond length while bending vibrations change the bond angle. These two classes may be subdivided into different types depending on how the atoms move relative to each other.
Vibrations of bonds involving hydrogen are an especially important diagnostic tool because atoms of low mass vibrate faster. The spectrum of n-octane, only has four major absorption bands at 2925, 1465, 1380, and 720 cm-1. What sort of vibrations comprise the four bands of a hydrocarbon?(3) We can understand the bands in n-octane by considering the following solution spectrum and Spartan simulation of methylene dichloride.
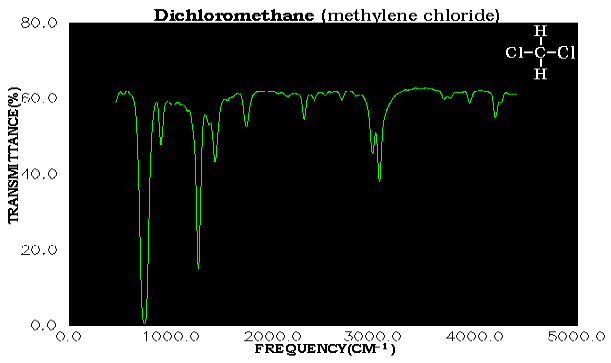
Assignment of peaks to a particular normal mode is not a trivial task. The NIST web site gives the gas phase peaks for CH2CL2 as: 3040, 2999, 1467, 1268, 1153, 898, 758, 717, 282 cm-1. The A2 band at 1153 is infrared-inactive and part of the noise in the base line. Conversely the most intense bands at 758 and 717 overlap to give one large peak. Finally there are additional bands due to impurities or combinations of the fundamental normal modes. Can you find all the bands corresponding to the nine fundamental modes?(4)
The nine normal modes of methylene dichloride are shown in the following table. Only the A1, B1, and B2 are infrared active while the A2 vibration is infrared inactive. A1 is an example of a symmetry label. They give us information about the symmetry of the vibration. A representations are symmetric to the highest order rotation axis of the molecule, while B representations are asymmetric to the rotation axis. What is the highest rotation axis of of this molecule?(5) You can change the view and rotate the molecule by putting the cursor into the molecule window and holding the right mouse key down to bring up a CHIME window. Select Display/Spacefill/Van der Waals Radii. Details of the calculation can be found in Spartan output. An awk script for making an xyz coordinate file of the vibration from the Spartan output file can be found in vibawk
|
Symmetric Stretching
3077 cm-1 A1 |
Asymmetric Stretching
3036 cm-1 B1 |
Scissoring (in-plane)
1327 cm-1 A1 |
|
Wagging (out-of-plane) 1241 cm-1 B2 |
Twisting (out-of-plane) 1056 cm-1 A2 |
Rocking (in-plane) 862 cm-1 B1 |
|
Chloride Vibrations Asymmetric Stretching 874 cm-1 B2 |
Chloride Vibrations Symmetric Stretching 773 cm-1 A1 |
Chloride Vibrations Scissoring 315 cm-1 A1 |
S.F. Sontum
Created 8/97
Updated 6/02