Lecture 16

1. A short story
2. Recursion
3. A simple example: raising a number to a power
4. A faster algorithm for calculating powers
5. Writing and understanding recursive programs
6. Another example: path finding

A short story

Recursion

A simple example: raising a number to a power

    /**
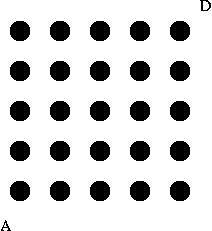
     *  @param exponent >= 0
     *  @returns base raised to exponent power
     **/ 
    public int simpleRecPower(int base, int exponent)
    {
       if (exponent == 0)
          return 1;
       else
          return base * simpleRecPower(base,exponent-1);
    }

How does this work? Clearly, if we evaluate simpleRecPower(3,0), the condition exponent==0 is true, so the method should return 1. Suppose instead we evaluate simpleRecPower(3,1). According to the method definition and the fact that 1!=0, we get that simpleRecPower(3,1) = 3*simpleRecPower(3,0), and we know the value of simpleRecPower(3,0) is 1. Thus the final answer is 3*1 or 3. The key is that we are using the facts that b⁰ = 1 and b^e+1 = b*b^e to calculate powers. Because we are calculating complex powers using simpler powers we eventually get to our base case.

A handy way of thinking about recursive programs is to think about having someone else handle the recursive call. So if I want to calculate simpleRecPower(3,5), I ask someone else to calculate simpleRecPower(3,4) and then, when they give me the answer, 81, multiply that answer by 3 to get the final answer of 243.

Of course we could also write this method with a while loop:

    /**
     *  @param exponent >= 0
     *  @returns base raised to exponent power
     **/ 
    public int simpleWhilePower(int base, int exponent)
    {
       int answer = 1;
       int counter = 1;
       while (counter <= exponent)
       {
          answer = answer * base;
          counter++;
       }
       return answer;
    }

If this is just as easily written using a while, why do we care about recursion? In some cases it provides us with a solution that is more elegant. That elegance can sometimes give us insights that help us to solve a problem more efficiently.

A faster algorithm for calculating powers

    /**
	@param exponent >= 0
	@returns base raised to exponent power
    **/ 
    public int fastPower(int base, int exponent) {
	if (exponent == 0) 
	    return 1
	else if (exponent%2 == 1)       // exponent is odd
	    return base * fastPower(base, exponent-1)
	else                            // exponent is even 
	    return fastPower(base * base, exponent / 2)
    }

In both of the programs given earlier, the number of multiplications necessary is equal to the value of the exponent. That is not the case here.

    fastPower(3,16) = fastPower(9,8)                 // mult
		    = fastPower(81,4)                // mult
		    = fastPower(6561,2)              // mult
		    = fastPower(43046721,1)          // mult
		    = 43046721 * fastPower(43046721,0)
		    = 43046721 * 1                   // mult
		    = 43046721

Thus it only took 5 multiplications (and 4 divisions by 2) using fastPower, whereas it would have taken 16 multiplications the other way (and divisions by two can be done very efficiently in binary).

In general it takes somewhere between log₂(exponent) and 2 * log₂(exponent) multiplications to compute a power this way. While this doesn't make a difference for small values of exponent, it does make a difference when exponent is large. For example, computing fastPower(3,1024) would only take 11 multiplications, while computing it the other way would take 1024 multiplications.

Why does this algorithm work? It works because it is based on the following simple rules of exponents:

• base⁰ = 1
• base^exp+1 = base*base^exp
• base^2*exp = (base²)^exp

The key is that by rearranging the order of doing things in a clever way, we can cut down the amount of work considerably! (Again it is possible to write the above algorithm with a while loop, but the above formulation is arguably easier to understand!)

Writing and understanding recursive programs

1. Write the base case. Convince yourself that this works correctly.
2. Write the "recursive" case.
   • Make sure all recursive calls go to simpler cases than the one you are writing. Make sure that the simpler cases will eventually get to a base case.
   • Make sure that the general case will work properly if all of the recursive calls work properly.

Another example: path finding

This problem (and path-finding problems in general) can be solved quite easily using recursion. We notice that from point A, the starting point, we must either pass through the point to our right or we must pass through the point above us (since we can't move diagonally). If we knew the number of paths from our right neighbor and the number of paths from our neighbor above, then all we have to do is add those together!

In general:

• If the start and end points are the same, there is only one path, and we're done.
• Otherwise, we check to see if we have a neighbor to our right and if so ask them for their number of paths. Then we check our neighbor to the north, if we have one, and add the numbers of neighboring paths together.

public int allPaths(int xStart, int yStart, int xEnd, int yEnd)
{
   // the number of paths from our neighbor to the right
   int xPaths = 0;
   // the number of paths from our neighbor above
   int yPaths = 0;
		
   // if the start point is the same as the end point, there's
   // only one path.
   if (xStart == xEnd && yStart == yEnd)
      return 1;
		
   // find out how many paths there are from the neighbor to the
   // right of the start point
   if (xStart < xEnd)
      xPaths = allPaths(xStart+1, yStart, xEnd, yEnd);
   // find out how many paths there are from the neighbor above
   if (yStart > yEnd)
      yPaths = allPaths(xStart, yStart-1, xEnd, yEnd);
			
   // add up the paths from each neighbor and return
   return xPaths + yPaths;		
}