Tuesday: Discuss "Computing Machinery and Intelligence" Mind: A Quarterly Review of Psychology and Philosophy, Volume LIX, Number 236: October 1950
 
 

Wednesday/Friday: "Breaking the Code" by Hugh Whitemore. Stageplay: 1986; Television adaptation: 1996.
 
 

Andrew Hodges: Alan Turing: the Enigma, (Walker and Company, New York), 2000.

(Alan Turing: The Enigma of Intelligence, Burnett Books, London, 1983)
 
 

http://www.turing.org.uk
 
 

Paul Strathern, Turing and the Computer, Anchor Books, New York, 1997.
 
 
 
 

The Collected Works of A. M. Turing

Mechanical Intelligence, ed. Darrel Ince, ISBN 0-444-88058-5, 1992

Morphogenesis, ed. P. T. Saunders, ISBN 0-444-88486-6, 1992

Pure Mathematics, ed. J. L. Britton, ISBN 0-444-88059-3, 1992

Mathematical Logic, ed. R. O. Gandy, C. E. M. Yates, ISBN: 0-444-50423-0, May 2001

North-Holland (Amsterdam; London).
 
 
 
 
 
 
 

1) He mapped out the theory of computers before a single computer had been conceived.

"On computable numbers, with an application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, Ser. 2 42 (1936), 230--265.

2) He broke the German Enigma Codes, saving Britain in World War II.

3) He established and set the agenda for the field of Artificial Intelligence.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

1912  1926-31 1930 1931-34     1932-35   1935	Birth, Paddington, London Sherborne School Death of friend Christopher Morcom  Undergraduate at King's College, Cambridge University Studies quantum mechanics, probability, logic Elected fellow of King's College, Cambridge
1936	The Turing machine; On Computable Numbers... submitted
1936-38	At Princeton University. Ph.D. Papers in logic, algebra, number theory
1938-39	Return to Cambridge. Introduced to German Enigma cipher problem
1939-40	Devises the Bombe, machine for Enigma decryption
1939-42	Breaking of U-boat Enigma cipher, saving battle of the Atlantic
1943-45	Chief Anglo-American consultant. Introduced to electronics
1945	National Physical Laboratory, London
1946	Computer design, leading the world, formally accepted
1947-48	Papers on programming, neural nets, and prospects for artificial intelligence
1948	Manchester University
1949	Work on programming and world's first serious use of a computer
1950	Philosophical paper on machine intelligence: the Turing Test
1951	Elected FRS. Paper on non-linear morphogenesis theory
1952	Arrested and tried as a homosexual, loss of security clearance
1953-54	Unfinished work in biology and physics
1954	Death by cyanide poisoning, Wilmslow, Cheshire.

 

The Halting Problem: Is it possible to create an "infinite loop detector" ?
 
 

Can a program be written that can analyze whether any program presented to it contains an infinite loop or not?

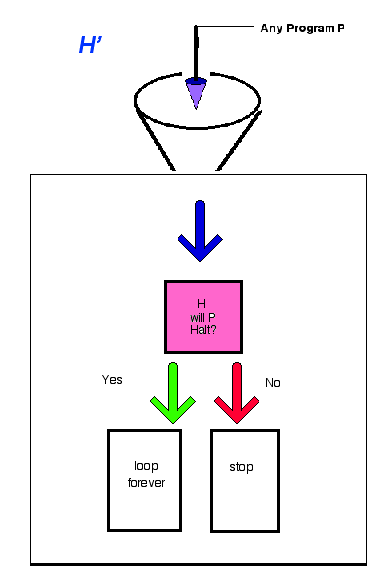
1) If a program P has no infinite loops

(that is, P eventually halts) then H' loops forever.
 

2) If a Program P has an infinite loop (that is, P does not halt), then H' halts.
 
 

(1) If H' has no infinite loops, then H' loops forever.

(2) If H' has infinite loop, then H' halts.
 
 

The Turing machine concept involves specifying a very restricted set of logical operations which are, however, sufficient to encompass anything that in modern terms would be called an algorithm.
 
 
 
 

Turing argued that his formalism was sufficiently general to encompass anything that a human being could do when carrying out a definite method.

He had the further idea of the Universal Turing Machine, capable of simulating the operation of any Turing machine.

A Universal machine is a Turing machine with the property of being able to read the description of any other Turing machine, and to carry out what

that other Turing machine would have done.

Turing gave an exact description of such a UTM in his paper

A Turing machine is a very simple machine, but, logically speaking, has all the power of any digital computer.

A Turing machine processes an infinite tape.

This tape is divided into squares, any square of which may contain a symbol from a finite alphabet, with the restriction that there can be only finitely many non-blank squares on the tape.
 
 
 

1

1

0

0

0

1

1

1

0

0

1

....

 

At any time, the Turing machine has a read/write head positioned at some square on the tape.

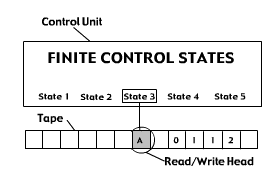
Furthermore, at any time, the Turing machine is in any one of a finite number of internal states. The Turing machine is further specified by a set of instructions of the following form:

(current_state, current_symbol, new_state, new_symbol, left/right)

This instruction means that if the Turing machine is now in current_state, and the symbol under the read/write head is current_symbol, change its

internal state to new_state, replace the symbol on the tape at its current position by new_symbol, and move the read/write head one square in the given

direction (left or right). If a Turing machine is in a condition for which it has no instruction, it halts.

Nowadays it is natural to think of the set of instructions as a program for the Turing machine.

There are several conventions commonly used in Turing machines We adopt the convention that numbers are represented in unary notation, i.e., that the non-negative integer n is represented by a string of n+1

successive 1's.

If we want to compute a function f(n1,n2, ... ,nk), we assume that initially the tape consists of n1, n2, ... , nk, properly encoded, with each separated from the previous one by a single blank, and with the tape head initially poised over the left-most bit of the first argument, and the state of the Turing machine some initial specified value.

We say that the Turing machine has computed

if, when the machine halts, the tape consists of n1, n2, ... , nk, , m, properly encoded, and separated by single blanks, and the read/write head back at the left-most bit of the first argument.

For example, suppose we wish to create a Turing machine to compute the function

m = multiply(n1,n2) = n1 * n2

Suppose the input tape reads

_<1>1 1 1 _ 1 1 1 1 1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

which encodes 3 and 4 respectively, in unary notation. (Here the position of the read/write head is marked.) Then the Turing machine should halt with its

tape reading

_<1>1 1 1 _ 1 1 1 1 1 _ 1 1 1 1 1 1 1 1 1 1 1 1 1 _ _ _ _ _

which encodes 3, 4, and 12 in unary notation.

The very simplicity of a Turing machine makes it a challenge to program one to perform a specific computation.

# Turing machine to multiply two numbers:

# Number n is represented by string of n+1 1's.

# Initially, tape is assumed to be in form of _n1_n2_ (where _ is blank),

# and head is assumed to be positioned at leftmost non-blank square.

# Initial internal machine state is "start".

# At halt, tape is _n1_n2_n3_, where n3=n1*n2,

# and head is positioned at leftmost non-blank square.

start, 1, move1right, W, R # mark first bit of 1st argument

move1right, 1, move1right, 1, R # move right til past 1st argument

move1right, _, mark2start, _, R # square between 1st and 2nd arguments found

mark2start, 1, move2right, Y, R # mark first bit of 2nd argument

move2right, 1, move2right, 1, R # move right til past 2nd argument

move2right, _, initialize, _, R # square between 2nd argument and answer found

initialize, _, backup, 1, L # put a 1 at start of answer

backup, _, backup, _, L # move back to leftmost unused bit of 1st arg

backup, 1, backup, 1, L # ditto

backup, Z, backup, Z, L # ditto

backup, Y, backup, Y, L # ditto

backup, X, nextpass, X, R # in position to start next pass

backup, W, nextpass, W, R # ditto

nextpass, _, finishup, _, R # if square is blank, we're done. finish up

nextpass, 1, findarg2, X, R # if square is not blank, go to work. mark bit

findarg2, 1, findarg2, 1, R # move past 1st argument

findarg2, _, findarg2, _, R # square between 1st and 2nd arguments

findarg2, Y, testarg2, Y, R # start of 2nd arg. skip this bit, copy rest

testarg2, _, cleanup2, _, L # if blank, we are done with this pass

testarg2, 1, findans, Z, R # if not, increment ans. mark bit, move there

findans, 1, findans, 1, R # still in 2nd argument

findans, _, atans, _, R # square between 2nd argument and answer

atans, 1, atans, 1, R # move through answer

atans, _, backarg2, 1, L # at end of answer--write a 1 here, go back

backarg2, 1, backarg2, 1, L # move left to first unused bit of 2nd arg

backarg2, _, backarg2, _, L # ditto

backarg2, Z, testarg2, Z, R # just past it. move right, and test it

backarg2, Y, testarg2, Y, R # ditto

cleanup2, 1, cleanup2, 1, L # move back through answer

cleanup2, _, cleanup2, _, L # square between 2nd arg and answer

cleanup2, Z, cleanup2, 1, L # restore bits of 2nd argument

cleanup2, Y, backup, Y, L # done with that. backup to start next pass

finishup, Y, finishup, 1, L # restore first bit of 2nd argument

finishup, _, finishup, _, L # 2nd argument restored, move back to 1st

finishup, X, finishup, 1, L # restore bits of 1st argument

finishup, W, almostdone, 1, L # restore first bit of 1st arg. almost done

almostdone, _, halt, _, R # done with work. position properly and halt

sample output:

GCCS = Goverment Code and Cipher School

A. Dilwyn Knox: Classical Scholar at Cambridge

Lytton Strachey

John Maynard Keynes

Bertrand Russell, Principia Mathematica

Kurt Gödel

David Hilbert

Ludwig Wittgenstein

Patricia Green = Joan Clarke

Alan Turing Memorial Sculptor: Glyn Hughes,  Contractors: Focus Arts	Andrew Hodges unveils Turing Plaque at his birthplace