CX 103: Introduction to Computers

Lecture 27
 
 

Today's Agenda

Cryptology and Computer Security


 

HTML/JavaScript Trick of the Day

A Simple on Screen Daily Calendar

SimpleCalendar.html

See Sections 13.8-9 for details on Date object.

<HTML>

<BODY BGCOLOR = "linen">

<SCRIPT LANGUAGE="JavaScript">

<!-- This script and many more are available free online at -->

<!-- The JavaScript Source!! http://javascript.internet.com -->

var Today=new Date();

var ThisDay=Today.getDay();

var ThisDate=Today.getDate();

var ThisMonth=Today.getMonth()+1;

var ThisYear=Today.getFullYear();

function DayTxt (DayNumber)

{

var Day=new Array();

Day[0]="Sunday"; Day[1]="Monday";

Day[2]="Tuesday"; Day[3]="Wednesday";

Day[4]="Thursday"; Day[5]="Friday";

Day[6]="Saturday";

return Day[DayNumber];

}

var DayName=DayTxt(ThisDay);

function MonthTxt (MonthNumber)

{

var Month=new Array();

Month[1]="January"; Month[2]="February";

Month[3]="March"; Month[4]="April";

Month[5]="May"; Month[6]="June";

Month[7]="July"; Month[8]="August";

Month[9]="September"; Month[10]="October";

Month[11]="November"; Month[12]="December";

return Month[MonthNumber];

}

var MonthName=MonthTxt(ThisMonth);

document.write("<TABLE BORDER=3 BGCOLOR=WHITE WIDTH=75 HEIGHT=85 align=left>"+"<TD>"+"<p align=center>"+"<font size=+1 >"+ "<EM>" + DayName+"<br>"+"<font color=orangered size=+3 >"+ThisDate+"</font>"+"<br>"+MonthName+"<br>"+"</b>"+"</font>"+"</p>"+"</TD>"+"</TR>"+"</TABLE>");

</SCRIPT> </HTML>


 
 
 
 

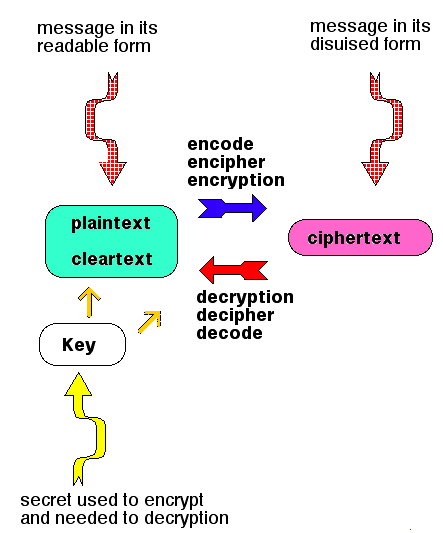
The Encryption Program

Encryption.html


 
 

Cryptology and Computer Security
 
 

Why Should You Be Interested in Cryptology?

Historical Importance

Military

Diplomatic

Contemporary Importance

Data Protection

Secure Communications

Governments

The Hotline

Banking and Funds Transfers

Email Privacy

Payments via Browsers

Cable TV and Scrambled Signals

Passwords and "Logging On"

Digital Cash and Smart Cards

Cellular Phones

The McVeigh Execution
 
 

Vehicle to Study Mathematical Topics


Number Theory Linear Algebra
Discrete Mathematics Computers
Probability and Statistics  

Intellectual Stimulation

Many Open Research Questions

Links to Other Disciplines

Engineering Linguistics

References

Simon Singh, The Code Book, Doubleday 1999.

David Kahn, The Codebreakers, Macmillan 1967; second edition, 1992.

David Kahn, Seizing the Enigma, Houghton-Mifflin, 1991.

Steven Budiansky, Battle of Wits: The Complete Story of Code Breaking in WWII, The Free Press, 2000.
 
 

Our Goal

Review some of the classic methods and learn enough about their underlying mathematics so we can appreciate the most important current public-key system: The RSA Algorithm,
 
 

CRYPTOLOGY

CRYPTOGRAPHY                                    CRYPTANALYSIS

Hiding the meaning                                            Discovering the meaning

of messages                                                          of intercepted messages
 
 

CRYPTOGRAPHY

A) HIDING THE EXISTENCE OF A MESSAGE

Steganography

Invisible Ink

Microdots

Pinholes
 
 

B) HIDING THE MEANING OF A MESSAGE

Transpositions

Substitutions


 
 

SUBSTITUTIONS

CODES

CIPHERS
 
 

CODES
 
plaintext ATTACK AT DAWN
coded text 15921 24586 49198

 

CIPHERS
 
 

Example: Replace each letter by the next one in the alphabet
 
plaintext ATTACK AT DAWN
ciphertext BUUBDL BU EBXO

 

CIPHERS

MONALPHABETIC SUBSTITUTION

POLYALPHABETIC SUBSTITUTION

POLYGRAPHIC SYSTEMS
 
 

MONALPHABETIC SUBSTITUTION

Caesar Cipher: Replace each letter of the message by the letter 3 places beyond it in the normal alphabet.
 
plaintext A B C D E F G H I J K L M
ciphertext D E F G H I J K L M N O P
                           
plaintext N O P Q R S T U V W X Y Z
ciphertext Q R S T U V W X Y Z A B C

 

AT T ACK AT DAWN

DWWDFN DW GD ZQ
 
 

Method: Shift by x characters

Key: value of x

Numerical Implementation

of Caesar Cipher

1) Replace each letter by its position in the alphabet

2) Add 3 % 26 to the position

3) Replace resulting number by its letter equivalent
 
 

M --> 13 --> 16 --> P
 
 

In JavaScript

Phrase is variable name; it contains a character string.

The first character in Phrase is Phrase.charAt(0);

Its ASCII value is ascii = Phrase.charCodeAt(0);

Its position in the alphabet is position = ascii - 64

To add 3 mod 26: cipherPosition =(position + 3) % 26

Now cipherPosition is the position of new letter in the alphabet.

Its ASCII value is x = cipherPosition + 64.

The corresponding letter is String.fromCharCode(x)
 
 

Summarizing:

ascii = Phrase.CharCodeAt(0);

position = ascii - 64;

cipherPosition =(position + 3) % 26

NewAscii = cipherPosition + 64

CipherCharacter = String.fromCharCode(NewAscii)

Caesar.html
 
 

Another View Of The Substiution Table


PlainText 

Character

 CipherText 

Character

   PlainText 

Character

 CipherText 

Character
A D   N Q
B E   O R
C F   P S
D G   Q T
E H   R U
F I   S V
G J   T W
H K   U X
I L   V Y
J M   W Z
K N   X A
L O   Y B
M P   Z C

 

Note that the red letters are just a rearrangement of the blue letters.

Any rearrangement of the alphabet produces another substitution scheme.

Here is another way to get a rearrangement;

Pick a key word: VERMONT

Make the letters the heads of columns in a table.

Fill in the rest of the alphabet into the table from left to right.
 
V E R M O N T
A B C D F G H
I J K L P Q S
U W X Y Z    

 

Then read the letters out of the table, column by column

going from left to right, reading each column from top to bottom:

VAIU EBJW RCKX MDLY OFPZ NGQ THS
 
 

This will be our arranged alphabet:

VAIUEBJWRCKXMDLYOFPZNGQTHS

The New Substiution Table


PlainText 

Character

 CipherText 

Character

   PlainText 

Character

 CipherText 

Character
A V   N D
B A   O L
C I   P Y
D U   Q O
E E   R F
F B   S P
G J   T Z
H W   U N
I R   V G
J C   W Q
K K   X T
L X   Y H
M M   Z S

 

Implementing Monoalphabetic Substitution

Encrypt:

(1) Find position of plaintext letter in straight

(2) Replace it with ciphertext in same position in mixed

Example: plaintext character is stored in PlainChar

position = straight.IndexOf(PlainChar)

CipherChar = mixed.charAt( position );

straight = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";

mixed = "VAIUEBJWRCKXMDLYOFPZNGQTHS";
 
 
 
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
V A I U E B J W R C K X M D L Y O F P Z N G Q T H S

 

Decrypt: Reverse the roles of straight and mixed.

KeywordCipher.html

How Many Rearrangements of the Alphabet are There?

26 * 25 * 24 * ... * 3 * 2 * 1 = 26!
 
 

26! is about 4 followed by 26 0's
 
 

We can use any of these monoalphabetic substitutions to encipher a message.

Suppose we intercept a message that was enciphered by using one of these schemes.

We try to "crack the code" by checking every possible scheme.

Would this work in theory?

Would in work in practice?
 
 
 
 

Suppose we could check 1,000,000 per second.

How long would it take to check them all?
 


How would you Break a Ciphered Message?

Suppose, first, you knew the basic method but not the particular key.

Example: It was done by a Caesar Cipher but you do not know the value of the shift.

Can try: "Exhaustive Search" = "Brute Force"
 
 
 
 

Example: It is a simple monoalphabetic substitution

but you do not know how the alphabet was scrambled.

Exhaustive Search is impractical.

What can we do?

Use the Cryptoanalyst's most powerful tool!

Frequency Analysis:

Frequency2.html
 
 

Standard Written English: Characteristic Frequencies

English Frequency and Sequence Data


Order and Frequency

of Single Letters:

 Order and Frequency of Leading Digrams
E 1231   L 403   B 162   TH 315   TO 111   SA 75   MA 56
T 959   D 365   G 161   HE 251   NT 110   HI 72   TA 56
A 805   C 320   V 93   AN 172   ED 107   LE 72   CE 55
O 794   U 310   K 52   IN 169   IS 106   SO 71   IC 55
N 719   P 229   Q 20   ER 154   AR 101   AS 67   LL 55
I 718   F 228   X 20   RE 148   OU 96   NO 65   NA 54
S 659   M 225   J 10   ES 145   TE 94   NE 64   RO 54
R 603   W 203   Z 9   ON 145   OF 94   EC 64   OT 53
H 514   Y 188       EA 131   IT 88   IO 63   TT 53
            TI 128   HA 84   RT 63   VE 53
            AT 125   SE 84   CO 59   NS 51
Group Percentages           ST 121   ET 80   BE 58   UR 49
            EN 120   AL 77   DI 57   ME 49
AEIOU   38.58%       OR 113   NG 75   RA 57   LY 47
LNRST   33.43%                    
JKQXZ   1.11%                    
ETAON   45.08%                    
ETAONISRH 70%                        

 

List of Common Reversals:


ER RE   ON NO   TE ET   ST TS
ES SE   IN NI   OR RO   IS SI
AN NA   EN NE   TO OT   ED DE
TI IT   AT TA   AR RA   OF FO

 
 
 

Order of Leading Trigrams in 10,000 letters of text:
 
THE ENT FOR NCE OFT    
AND ION NDE EDT STH    
THA TIO HAS TIS MEN    

 

Order of Letters as Initial Letters of Words:

T A S O I C W P B F H M R E N L G U Y V J K Q X Z

Order of Letters as Final Letters of Words:

E S D N T R Y O F L A G H M W K C P I X U B V J Z Q
 
 


Standard Written English


E the highest frequency
T A O I N S H R high frequency group
D L medium frequency
C U M W F G Y P B low frequency
V K J X Q Z rare

 

Notes:

(1) Use for "Wheel of Fortune"

(2) Frequencies in other languages vary from English

(3) Frequency.html can be used to count characters.
 
 

With a Caesar Cipher, we only need to know where one letter goes to find the key (since all other letters are shifted the same amount)

How to Use Frequency Analysis

For Caesar Cipher: Do a frequency analysis of the ciphertext. Guess that E was shifted to the most frequent letter and try this shift as the key. Your guess should also be consistent with the following observations about standard written English:

Among High Frequency Letters:

A, E, I are 4 apart (equally spaced)

R, S, T from a consecutive triple

Among Low Frequency Letters;

V, W, X, Y, Z are 5 consecutive lows.

What happens to these patterns under a shift?

Aside: The frequency of individual letters is known as a "first order statistic." Pairs of letters that occur together are called digrams or digraphs while triples are called trigrams or trigraphs. The frequencies of these higher order statistics are also useful:

The Federalist Papers

Shakespeare

Hemingway

Deep Throat

Primary Colors

Why Don't All Letters Appear With Same Frequency?




Pl_dging eq_al sup_ort to d_moc_acy and fr__ trad_, l_ad_rs of th_ W_st_rn H_misph_r_ c_os_d a su_mit m__ting to_ay by r_infor_in_ th_ir commitm_nt to a vast Fr__ Trad_ Ar_a of th_ Am_ricas, vo_ing to _nsur_ that its b_n_fits ar_ shar_d by th_ h_misph_r_'s _ight h_ndr_d mill_on p_opl_.

"Th_r_'s no qu_stion in my mi_d tha_ w_ hav_ chall_ng_s ah_ad of us, but th_r_'s also no qu_sti_n in _y m_nd that w_ can m__t thos_ chall_ng_s," Pr_sid_nt Bu_h sa_d aft_r h_ and th_ oth_r l_ad_rs sign_d a clo_ing d_clarati_n.
 
 


Redundancy
 
 
 
 
 
 


 

Numerical Implementation

of the Caesar Cipher

using Modular Arithmetic



Modular Arithmetic:

25 % 3 = 1 means 1 is the remainder when 25 is divided by 3.

Uses of Modular Arithmetic we've seen:

Stripping off digits of a number (% 10)

Finding binary representation of a number (% 2)

Determining if an integer is odd or even (% 2)
 
 
 
 

Telling Time: In "clock arithmetic" there are only 12 numbers (hours):

0 (=12) 1 2 3 4 5 6 7 8 9 10 11

In clock arithmetic (% 12)

5 + 10 = ______

2 - 5 = _______

-5 = ________

Clock Arithmetic is denoted Z12

Life in Z12 has some familiar features but some things are very different:

-5 = 7 (the "negative" of a number may be bigger than the number!).

2 * 6 = 0 (The product of two nonzero numbers may = 0)

5 * 5 = 1 so = 5. The reciprocal of 5 is 5 (multiplicative inverse)

Not every number has an inverse:

The equation 2x = 1 has no solution in Z12
 
 
 
 
 
 
 
 

Caesar Cipher is done with arithmetic Modulo 26.

Represent letters by their position in alphabet
 
 
 
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

If we shift by 14, then

S --> 19 --> 19 + 14 = 33 % 26 = 7 --> G