CX 103: Introduction
to Computers

Lecture
23

Second
Exam: Tomorrow
Focus
of Exam
JavaScript
Fire
in the Valley: Chapters 5 - 8
Closed
Books & Notes, but
can
bring 1 sheet of scribblings


Volunteer
Opportunity
Design a Web Page for
The Middlebury Fire
Department

Jennie Diggins
Volunteer Coordinator
Community Service Office
Middlebury College
802-443-3099

Searching
Arrays
Linear
Search
Verbal Description:
Compare Target with first element in the array
If identical, stop.
Otherwise move to the next element
Repeat
Recursive Approach (Basic Idea)
LinearSearch(Low,High)
if (Target == TheArray[Low] ) STOP;
else LinearSearch(Low+1, Search)
(Need to clean up to handle what happens if Low = High
and Target not yet found)
LINEAR SEARCH
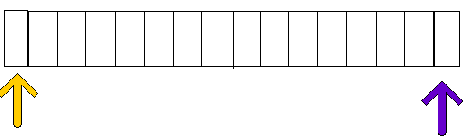
INITIAL STEP
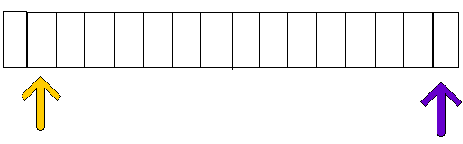
AFTER 1 STEP
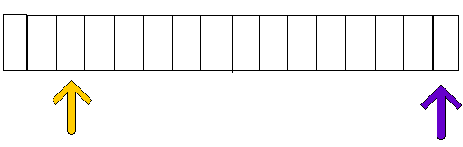
AFTER 2 STEPS

Binary Search
Verbal Description:
Is Target >= Middle Element of current List?
If "Yes" then throw away bottom half of list
If "No" then throw away top half of list
Repeat until list has one element.
Is Target = remaining element?
function Binary(Low,High)
{ (provide escape clause
when High = Low+1) else
Middle = Math.floor( (Low
+ High)/2 );
if ( Target >= TheArray[Middle]
)
Low = Middle;
else High = Middle;
Binary(Low, High);
BINARY SEARCH
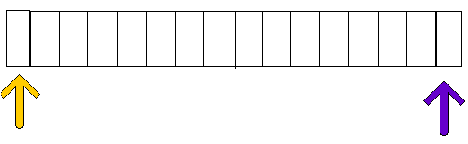
INITIAL STEP
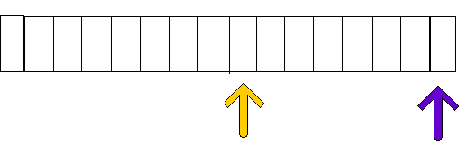
AFTER 1 STEP
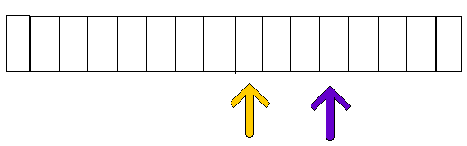
AFTER 2 STEPS
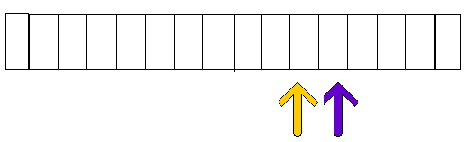
AFTER 3 STEPS

Example: Is Homer in the
List?
List is:
| 1)
Andrew |
9)
Colin |
17)
Kennan |
25)
Rebecca |
| 2)
Annalise |
10)
DavidM |
18)
Liz |
26)
RyanB |
| 3)
Beth |
11)
DavidR |
19)
Louisa |
27)
RyanP |
| 4)
Bob |
12)
DavidS |
20)
Matt |
28)
Ted |
| 5)
Brendan |
13)
Eliza |
21)
Megan |
29)
Tejas |
| 6)
Casey |
14)
John |
22)
Missy |
30)
Trevor |
| 7)
CharlesM |
15)
Jordan |
23)
Nathaniel |
31)
Tyler |
| 8)
CharlesR |
16)
Kate |
24)
Rada |
32)
Veljko |
Step 1: Could Target be
in second half of the list?
Is Homer >= Name[17]?
Is Homer >= Kennan?
No
List is:
| 1)
Andrew |
9)
Colin |
| 2)
Annalise |
10)
DavidM |
| 3)
Beth |
11)
DavidR |
| 4)
Bob |
12)
DavidS |
| 5)
Brendan |
13)
Eliza |
| 6)
Casey |
14)
John |
| 7)
CharlesM |
15)
Jordan |
| 8)
CharlesR |
16)
Kate |
Step 2: Could Target be
in second half of the list?
Is Homer >= Name[9]?
Is Homer >= Colin?
Yes
List is:
| 9) Colin |
| 10) DavidM |
| 11) DavidR |
| 12) DavidS |
| |
| 13) Eliza |
| 14) John |
| 15) Jordan |
| 16) Kate |
Step 3: Could Target be
in second half of the list?
Is Homer >= Name[13]?
Is Homer >= Eliza?
Yes
List is:
| 13) Eliza |
| 14) John |
| |
| 15) Jordan |
| 16) Kate |
Step 4: Could Target be
in second half of the list?
Is Homer >= Name[15]?
Is Homer >= Jordan?
NO
List is:
Step 5: Could Target be
in second half of the list?
Is Homer >= Name[14]?
Is Homer >= John?
NO
List is:
Step 6: Is Target the
remaining element?
Is Homer = Name[13]?
Is Homer = Eliza?

Example: Is Ted in the
List?
List is:
| 1)
Andrew |
9)
Colin |
17)
Kennan |
25)
Rebecca |
| 2)
Annalise |
10)
DavidM |
18)
Liz |
26)
RyanB |
| 3)
Beth |
11)
DavidR |
19)
Louisa |
27)
RyanP |
| 4)
Bob |
12)
DavidS |
20)
Matt |
28)
Ted |
| 5)
Brendan |
13)
Eliza |
21)
Megan |
29)
Tejas |
| 6)
Casey |
14)
John |
22)
Missy |
30)
Trevor |
| 7)
CharlesM |
15)
Jordan |
23)
Nathaniel |
31)
Tyler |
| 8)
CharlesR |
16)
Kate |
24)
Rada |
32)
Veljko |
Step 1: Could Target be
in second half of the list?
Is Ted >= Name[17]?
Is Ted >= Kennan?
Yes
List is:
| 17)
Kennan |
25)
Rebecca |
| 18)
Liz |
26)
RyanB |
| 19)
Louisa |
27)
RyanP |
| 20)
Matt |
28)
Ted |
| 21)
Megan |
29)
Tejas |
| 22)
Missy |
30)
Trevor |
| 23)
Nathaniel |
31)
Tyler |
| 24)
Rada |
32)
Veljko |
Step 2: Could Target be
in second half of the list?
Is Ted >= Name[25]?
Is Ted >= Rebecca?
Yes
List is:
| 25) Rebecca |
| 26) RyanB |
| 27) RyanP |
| 28) Ted |
| |
| 29) Tejas |
| 30) Trevor |
| 31) Tyler |
| 32) Veljko |
Step 3: Could Target be
in second half of the list?
Is Ted >= Name[29]?
Is Ted >= Tejas?
No
List is:
| 25) Rebecca |
| 26) RyanB |
| |
| 27) RyanP |
| 28) Ted |
Step 4: Could Target be
in second half of the list?
Is Ted >= Name[27]?
Is Ted >= RyanP?
Yes
List is:
Step 5: Could Target be
in second half of the list?
Is Ted >= Name[27]?
Is Ted >= Ted?
NO
List is:
Step 6: Is Target the
remaining element?
Is Ted = Name[28]?
Is Ted = Ted?
Does Binary Search
Work?
Is it Efficient?
If it takes 6 steps
to search a list of
32 names, how many
steps does it take to search a list of 64 names?
Each doubling of the
list size only increases the number of comparisons by 1.
With n comparisons,
we can search an ordered list of 2^n elements.
| Array
size |
Number
of steps |
| 1000 |
10 |
| 1,000,000 |
20 |
| 1,000,000,000 |
30 |
BinarySearch.html
BinarySearch2.html
BinarySearch3.html

Multiple-Subscripted
Arrays
Arrays and Computer
Dating Services
| |
#1 |
#2 |
#3 |
#4 |
#5 |
#6 |
#7 |
#8 |
#9 |
#10 |
| Andrew |
Yes |
No |
No |
Yes |
Yes |
Yes |
Yes |
No |
No |
No |
| Annalise |
Yes |
Yes |
Yes |
No |
No |
Yes |
No |
No |
Yes |
Yes |
| Beth |
Yes |
Yes |
No |
No |
Yes |
No |
Yes |
Yes |
Yes |
Yes |
| Bob |
No |
Yes |
Yes |
Yes |
No |
No |
No |
Yes |
No |
No |
| Brendan |
Yes |
No |
Yes |
Yes |
Yes |
No |
No |
Yes |
Yes |
Yes |
| Casey |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
| Charles
M |
Yes |
No |
No |
Yes |
Yes |
No |
Yes |
Yes |
No |
Yes |
| Charles
R |
No |
Yes |
No |
Yes |
Yes |
No |
No |
Yes |
No |
No |
| Colin |
Yes |
Yes |
Yes |
No |
No |
No |
Yes |
Yes |
Yes |
Yes |
| David
M |
Yes |
No |
Yes |
Yes |
No |
Yes |
No |
Yes |
Yes |
No |
| David
R |
No |
No |
No |
No |
No |
Yes |
Yes |
Yes |
Yes |
No |
| David
S |
Yes |
No |
No |
Yes |
No |
Yes |
No |
No |
No |
Yes |
| Eliza |
Yes |
Yes |
No |
Yes |
Yes |
No |
No |
Yes |
Yes |
Yes |
| John |
No |
Yes |
No |
Yes |
Yes |
No |
Yes |
No |
No |
Yes |
| Jordan |
Yes |
Yes |
No |
Yes |
Yes |
No |
Yes |
No |
Yes |
No |
| Kate |
Yes |
No |
No |
No |
No |
No |
Yes |
Yes |
No |
Yes |
| Kennan |
Yes |
Yes |
No |
No |
No |
No |
No |
Yes |
No |
Yes |
| Liz |
No |
Yes |
No |
Yes |
Yes |
No |
No |
No |
Yes |
Yes |
| Louisa |
Yes |
No |
No |
Yes |
No |
No |
Yes |
Yes |
No |
No |
| Matt |
No |
Yes |
No |
No |
Yes |
Yes |
No |
Yes |
Yes |
No |
| Megan |
Yes |
No |
No |
Yes |
Yes |
Yes |
Yes |
No |
Yes |
No |
| Missy |
No |
No |
No |
Yes |
No |
No |
No |
Yes |
No |
No |
| Nathaniel |
Yes |
No |
No |
No |
Yes |
No |
No |
Yes |
No |
Yes |
| Rada |
No |
No |
Yes |
Yes |
Yes |
No |
Yes |
Yes |
Yes |
Yes |
| Rebecca |
No |
Yes |
No |
Yes |
No |
No |
No |
Yes |
No |
Yes |
| Ryan
B |
Yes |
No |
Yes |
Yes |
Yes |
Yes |
No |
No |
Yes |
No |
| Ryan
P |
Yes |
Yes |
No |
No |
Yes |
No |
No |
No |
Yes |
Yes |
| Ted |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
Yes |
Yes |
Yes |
| Tejas |
Yes |
No |
Yes |
Yes |
No |
No |
Yes |
Yes |
Yes |
No |
| Trevor |
No |
Yes |
No |
Yes |
No |
Yes |
Yes |
No |
No |
Yes |
| Tyler |
No |
Yes |
No |
No |
No |
No |
Yes |
Yes |
Yes |
No |
| Veljko |
No |
Yes |
Yes |
Yes |
No |
No |
Yes |
No |
No |
Yes |
| |
|
|
|
|
|
|
|
|
|
|

| Casey |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
| Eliza |
Yes |
Yes |
No |
Yes |
Yes |
No |
No |
Yes |
Yes |
Yes |
4 |
| Casey |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
| Louisa |
Yes |
No |
No |
Yes |
No |
No |
Yes |
Yes |
No |
No |
5 |
| Brendan |
Yes |
No |
Yes |
Yes |
Yes |
No |
No |
Yes |
Yes |
Yes |
| Casey |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
No |
Yes |
Yes |
6 |
Array of 32 students
Each student is represented
by an array of 11 elements

An Array of Arrays
<HTML>
<HEAD>
<TITLE>Presidents</TITLE>
<SCRIPT LANGUAGE = "Javascript">
var President = new Array(5);
for (i = 0; i <= 4;
i = i + 1)
President[i] = new Array(3);
President[0] [0] = "Name"
President[0] [1] = "Home
State"
President[0] [2] = "Year
Elected"
President[1] [0] = "Ronald
Reagan"
President[1] [1] = "California"
President[1] [2] = "1980,
1988"
President[2] [0] = "George Bush"
President[2] [1] = "Maine"
President[2] [2] = "1988"
President[3] [0] = "Bill Clinton"
President[3] [1] = "Arkansas"
President[3] [2] = "1992, 1996"
President[4] [0] = "George W. Bush"
President[4] [1] = "Texas"
President[4] [2] = "2000"
document.writeln("<TABLE
BORDER = '2' WIDTH = '100%' > ") ;
for (i = 0; i <= 4;
i = i + 1)
{ for (j=0; j<=2; j=j+1)
document.writeln("<TD><H1>"
+ President[i][j] + "</TD>");
document.writeln("<TR>");
}
document.writeln(" </TABLE> ");
</SCRIPT>
</HEAD>
<BODY BGCOLOR = "cadetblue">
</BODY>
</HTML>
Presidents.html









