CX 103: Introduction to Computers
 
 

Lecture 20


 
 

Date of Second Exam: Tuesday, April 17

Encryption Scheme Exercise

Isolating the digits of a four digit number: N = abcd

Method 1

d = N % 10

N = (N - d)/10 abc0/10 = abc

c = N % 10

N = (N-c)/10 ab0/10 = ab

b = N % 10

N = (N-b)/10 a0/10 = a

a = N % 10
 
 
 
 

Method 2:Use Math.floor function

Math.floor(X) = integer part of X

Math.floor(19.83) = 19

d = N % 10

c = ( Math.floor(N/10) ) % 10 Math.floor( abc.d ) = abc

b = ( Math.floor(N/100) % 10 Math.floor(ab.cd) = ab

a = ( Math.floor(N/1000) % 10 Math.floor(a.bcd) = a
 
 


 
 

Functions in JavaScript

Outline

Introduction

Program Modules in JavaScript

Programmer-Defined Functions

Function Definitions

Random Number Generation

Modularization

Simulation

Duration of Identifiers

Scope Rules

Recursion
 
 

Recursion

One function may call another function.

Can a function call itself?

Yes!

A very powerful idea.

Must be used with care.

Infinite Loops possible
 
 

Too much recursing can be dangerous!


The Classic Application of Recursion

Factorials

6! = 6 * 5 * 4 * 3 * 2 * 1 = 720

N! = N * (N-1) *(N-2) *...*3*2*1

N! is the product of the first N positive integers
 
 

<HTML>

<HEAD>

<TITLE>Factorial via For Loop </TITLE>

<SCRIPT LANGUAGE = "JavaScript">

function factorial(N)

{ var S,i;

    S = 1;

    for (i = 1; i <= N; i = i + 1)

    S = S * i;

    return S;

}

Number = window.prompt("Enter a Positive Integer", " ");

Number = parseInt(Number)

document.writeln( "<H1>The factorial " + Number +"! is " + factorial(Number) );

</SCRIPT>

<BODY BGCOLOR = "salmon"> </BODY> </HTML> factorial2.html

Recursive Approach

6! = 6 * 5 * 4 * 3 * 2 * 1 = 6 * (5!)

factorial(6) = 6 * factorial(5)

N! = N * (N-1) *(N-2) *...*3*2*1

= N * [(N-1) *(N-2) *...*3*2*1 ]

= N * (N-1)!

so factorial(N) = N * factorial(N-1)
 


 

<HTML>

<HEAD>

<TITLE>Factorial via Recursion </TITLE>

<SCRIPT LANGUAGE = "JavaScript">
 
 

function factorial(N)

{

if (N == 1) return 1;

else return N* factorial(N-1)

}
 
 

Number = window.prompt("Enter a Positive Integer", " ");

Number = parseInt(Number)

document.writeln( "<H1>The factorial " + Number +"! is " + factorial(Number) );
 
 

</SCRIPT>

<BODY BGCOLOR = "salmon"> </BODY>

</HTML>

factorial.html

Another Application of Recursion

Converting Decimal to Binary

<HTML>

<HEAD>

<TITLE>Converting From Decimal to Binary </TITLE>

<SCRIPT LANGUAGE = "JavaScript">

N = parseInt(window.prompt("Enter N", "") );

Convert(N);

function Convert(N)

{

if (N != 0)

{ Convert(Math.floor(N/2) );

document.writeln(N % 2) ; }

}

</SCRIPT>

</HEAD>

<BODY BGCOLOR = "white"> </BODY>

</HTML>
 
 

convert.html

<HTML>

<HEAD>

<TITLE>Convert From Decimal to Arbitrary Base</TITLE>

<SCRIPT LANGUAGE = "JavaScript">

N = parseInt(window.prompt("Enter number to convert from base 10 ", "") );

Base =parseInt(window.prompt("Enter new Base:", " ") );

document.writeln(N + " in base 10 becomes, in base " + Base + " the number " );

Convert(N);

function Convert(N)

{

if (N != 0)

{ Convert(Math.floor(N/Base ));

document.writeln(N % Base) ; }

}

</SCRIPT>

</HEAD>

<BODY BGCOLOR = "white"> </BODY>

</HTML>

convert2.html

Towers of Hanoi

TowersOfHanoi.html
 
 

Let's determine first the number of moves it takes to transfer n disks.

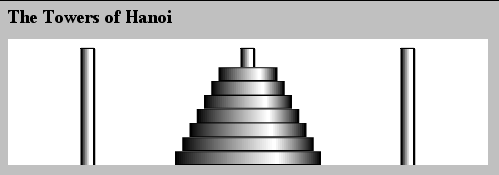
Goal: Move n disks from Pole A to Pole C:

Recursive Idea

if n = 1, then just do it. (1 move)

if n > 1, then

move (n-1) disks from A to B

move last disk from A to C

move (n-1) disks from B to C

Let Moves(n) be the number of moves it takes to transfer n disks.

Thus Moves(n) = Moves(n-1) + 1 + Moves(n-1)

so Moves(n) = 1 + 2*Moves(n-1)


<HTML>

<HEAD>

<TITLE>Number of Hanoi Moves </TITLE>

<SCRIPT LANGUAGE = "Javascript">

var Disks;

Disks = window.prompt("How many disks?","");

Disks = parseInt(Disks);

function NumberMoves(N)

{ if (N == 1) return 1;

else return 1 + 2*NumberMoves(N-1)

}

document.writeln("To move " + Disks + " disks takes " + NumberMoves(Disks) + " moves.");

</SCRIPT>

</HEAD>

<BODY BGCOLOR = "white"> </BODY>

</HTML>

HanoiMoves.html


<HTML>

<HEAD> <TITLE>Towers of Hanoi</TITLE>

<SCRIPT LANGUAGE = "JavaScript">

function MoveDisk(fromPeg, toPeg)

{ document.writeln("Move Disk from " + fromPeg + " to " + toPeg + "<BR>");

}

function hanoi(N, fromPeg, toPeg, helpPeg)

{

if (N == 1)

MoveDisk( fromPeg, toPeg);

else

{ hanoi(N-1, fromPeg, helpPeg, toPeg);

MoveDisk( fromPeg, toPeg);

hanoi(N-1, helpPeg, toPeg, fromPeg) };

}

Disks = window.prompt("Enter Number of disks", "");

Disks = parseInt(Disks);

hanoi(Disks, "A", "B", "C");

</SCRIPT>

</HEAD>

<BODY BGCOLOR = "white"> </BODY>

</HTML>
 Hanoi.html

Assignment 20





3) Write a recursive function which takes an integer value and returns the number with the digits reversed. For example, given the number 13452, the function should return 25431. Incorporate the function into a script that prompts a value from the user. The script should be able to handle an integer with any number of digits (including one). The user simply inputs the number; the user is not asked to tell the program how many digits are in the number.

Recursive Idea:

Chop off units digit

Reverse the rest

Example : 1983

chop off 3: 1983 reverse 198

chop off 8: 198 reverse 19

chop off 9: 19 reverse 1

chop off 1: 1

Arrays

Consider a stringin JavaScript.

It is a sequenceof characters

W = window.prompt("Enter something", "");

Suppose user types in Middlebury

W = Middlebury
 
M i d d l e b u r y
W[0] W[1] W[2] W[3] W[4] W[5] W[6] W[7] W[8] W[9]

<HTML>

<HEAD>

<TITLE>Arrays </TITLE>

<SCRIPT LANGUAGE = "Javascript">

W= window.prompt("Enter a word","");

document.writeln("<H1>The word you gave me was " + W);

document.writeln("<BR>The individual characters are ");

for (i = 0; i <= 9; i = i + 1)

document.writeln("<BR>" + W[i]);

</SCRIPT>

</HEAD>

<BODY BGCOLOR = "white"> </BODY>

</HTML>

array1.html

What if we don't know the length of the word?

W.length tells us.

<HTML>

<HEAD>

<TITLE>Arrays </TITLE>

<SCRIPT LANGUAGE = "Javascript">

W= window.prompt("Enter a word","");

document.writeln("<H1>The word you gave me was " + W);

document.writeln("<BR>The individual characters are ");

for (i = 0; i <= W.length - 1; i = i + 1)

document.writeln("<BR>" + W[i]);

</SCRIPT>

</HEAD>

<BODY BGCOLOR = "white">

</BODY>

</HTML>

array3.html

Writing a string backwards

<HTML>

<HEAD>

<TITLE>Arrays </TITLE>

<SCRIPT LANGUAGE = "Javascript">

W= window.prompt("Enter a word","");

document.writeln("<H1>The word you gave me was " + W);

document.writeln("<BR><BR>Now we will write it backwards:<BR>");

for (i = W.length-1; i >= 0; i = i - 1)

document.write(W[i]);

</SCRIPT>

</HEAD>

<BODY BGCOLOR = "white">

</BODY>

</HTML>

array4.html